Вниманию читателя предлагается алгоритм вычисления логарифма по основанию 2, предоставляется исходный код RTL-блока, анализируется вычислительная точность и ресурсоемкость реализации.
В математических вычислениях и цифровой обработке сигналов на ПЛИС часто приходится прибегать к вычислению логарифма. Например, для преобразования мощности из мВт в дБм требуется вычисление логарифма по основанию 10:
PdBm=10 * log10(PмВт ⁄ 1мВт)
Вычисление логарифма является достаточно актуальной задачей, разработчики применяю разные методы вычисления [1]:
- табличный метод;
- итерационный метод;
- CORDIC метод;
- метод на основе рядов Тейлора.
Методы различаются точность, сложностью реализации и задержкой вычисления. Вниманию предлагается реализация итерационного метода вычисления логарифма по основанию 2 с фиксированной точкой. Вычисление log2(X) проще в реализации, чем вычисление натурального ln(X) или десятичного log10(X). А преобразовать к логарифму с нужным основанием всегда можно всего через одно умножение: logAB=logCB ⁄ logCA .
В статье описывается алгоритм вычисления с примерами, предоставляется исходный код RTL-блока, анализируется вычислительная точность и ресурсоемкость реализации.
Алгоритм
Представим входное значение X через мантиссу m и экспоненту e следующим образом:
X=me2
Логарифм от X может быть представлен, как сумма целой e и дробной log2m составляющих
Y = log2X = e + log2m
Тогда алгоритм вычисления можно представить блок-схемой на рисунке 1. Сначала параллельно вычисляется экспонента e и мантисса m, затем из мантиссы m логарифмическим преобразованием находится L = log2(m), и в конце результаты суммируются.
Вычисление экспоненты e и мантиссы m можно представить блок-схемой на рисунке 2. Процесс вычисления e и m выполняется следующим образом:
- Определяется диапазон входного значения Х – больше 1 или нет.
- Если больше 1, то Х итерационно делится на 2 до тех пор, пока не станет меньше 2. Число итераций непосредственно определяет экспоненту e. Если меньше 1, то Х итерационно умножается на 2 до тех пор, пока не станет больше 1. Число итераций определяет экспоненту e с инверсией знака.
- Мантисса m является X после итераций умножения или деления.
Получив мантиссу m можно вычислить log2(m) посредством логарифмического преобразования в соответствии с блок-схемой на рисунке 3. Процесс логарифмического преобразования выполняется следующим образом:
- Запускается итерационный процесс с фиксированным числом шагов, равным требуемой разрядностью дробной части. На каждой итерации мантисса m возводится в квадрат.
- Если мантисса m больше или равна 2, то m делится на 2 и к результату L суммируется 2-i, где i – номер итерации; иначе - ничего.
- По окончании итерационного процесса результатом логарифмического преобразования будет L = log2(m).
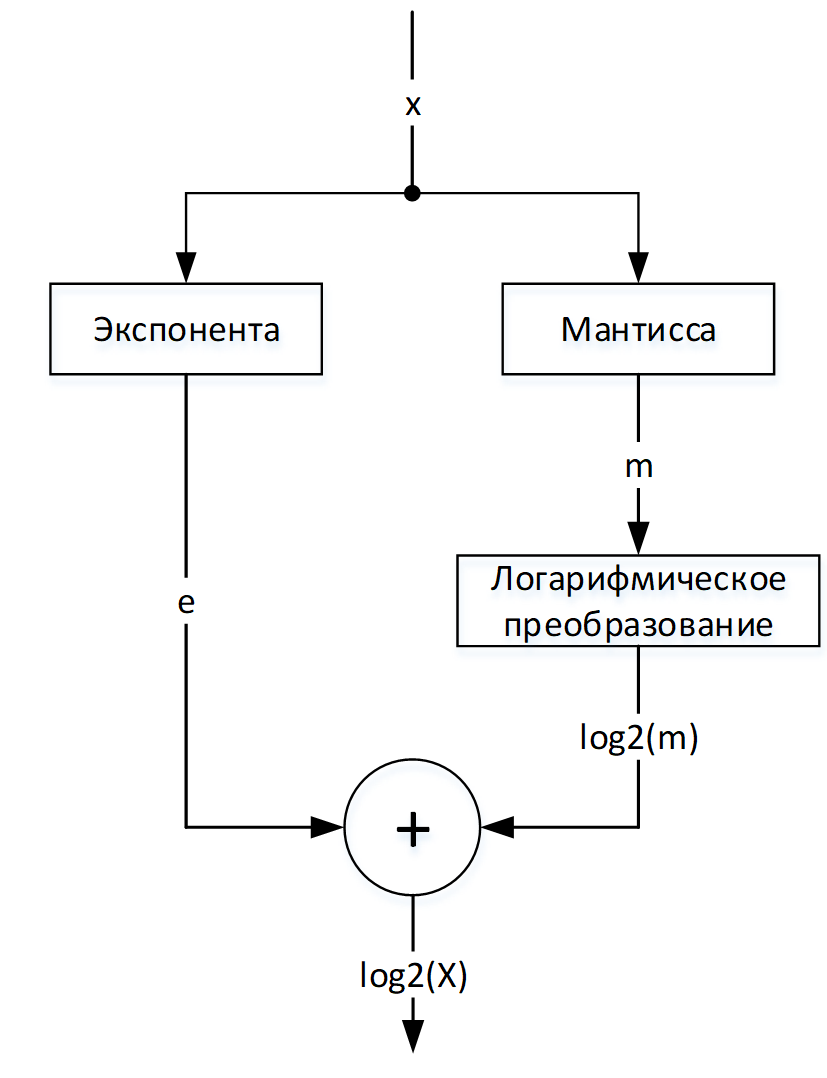
Рисунок 1 – Блок-схема вычисления log2(x)
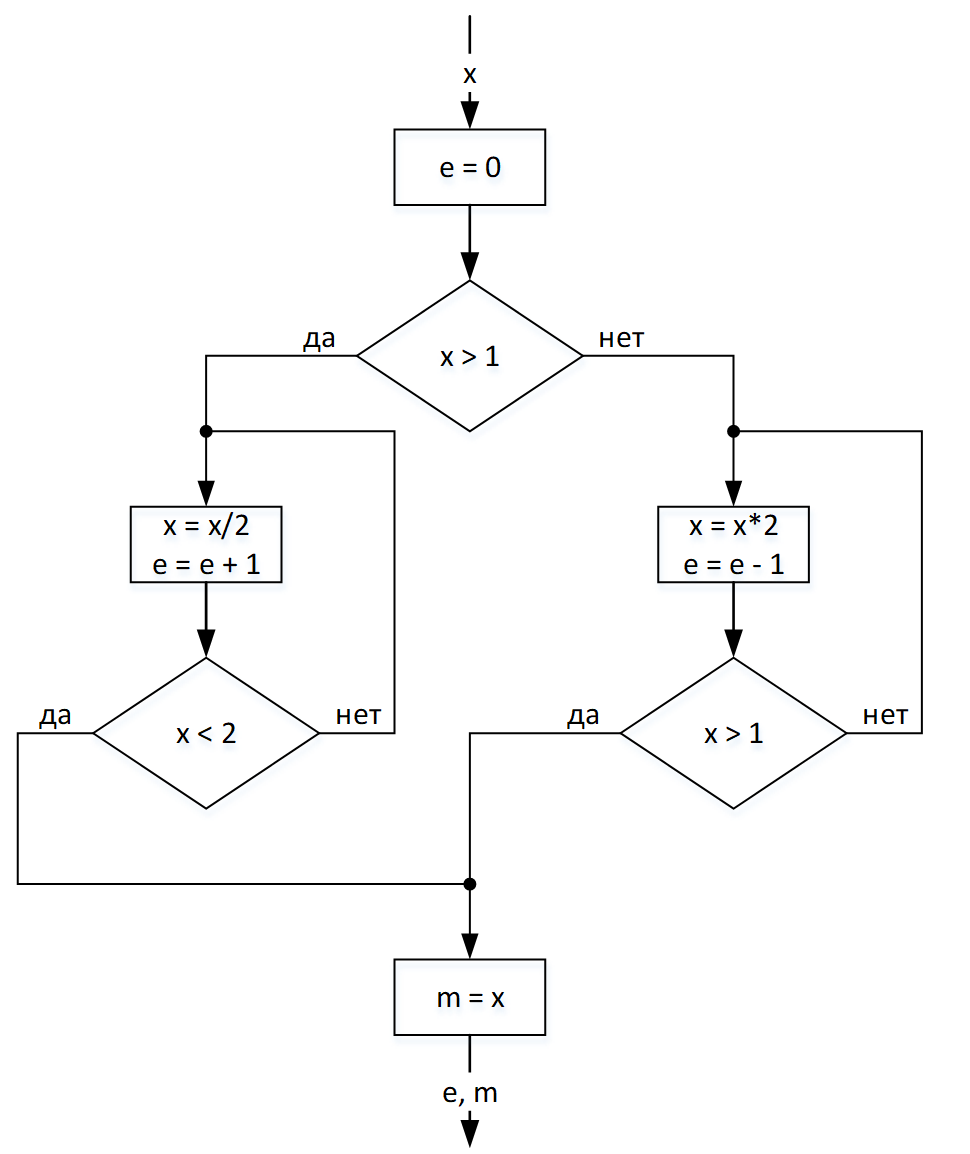
Рисунок 2 – Блок-схема вычисления экспоненты и мантиссы
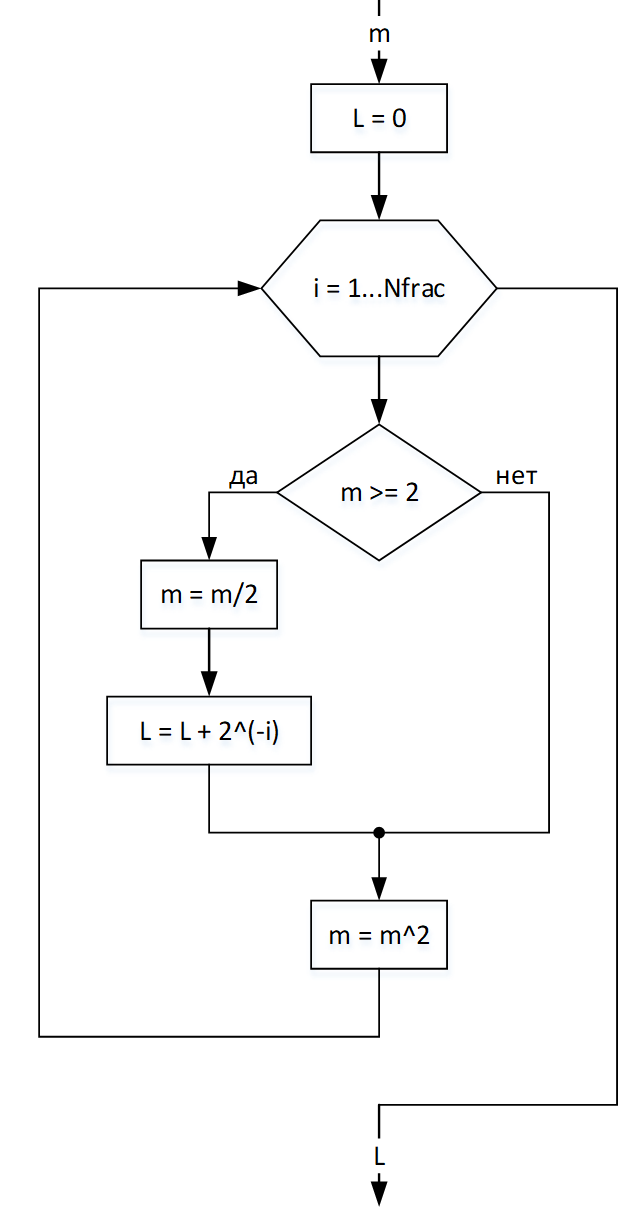
Рисунок 3 – Блок-схема логарифмического преобразования
Пример №1
Дано:
- Входное значение X = 10,23456789
- Точность (разрядность дробной части) – 10 бит.
Решение:
1. Вычисление e и m
Поскольку X > 1, значит производится деление. e = 0.

Экспонента e = 3.
Мантисса m = 1,2793.
2. Логарифмическое преобразование
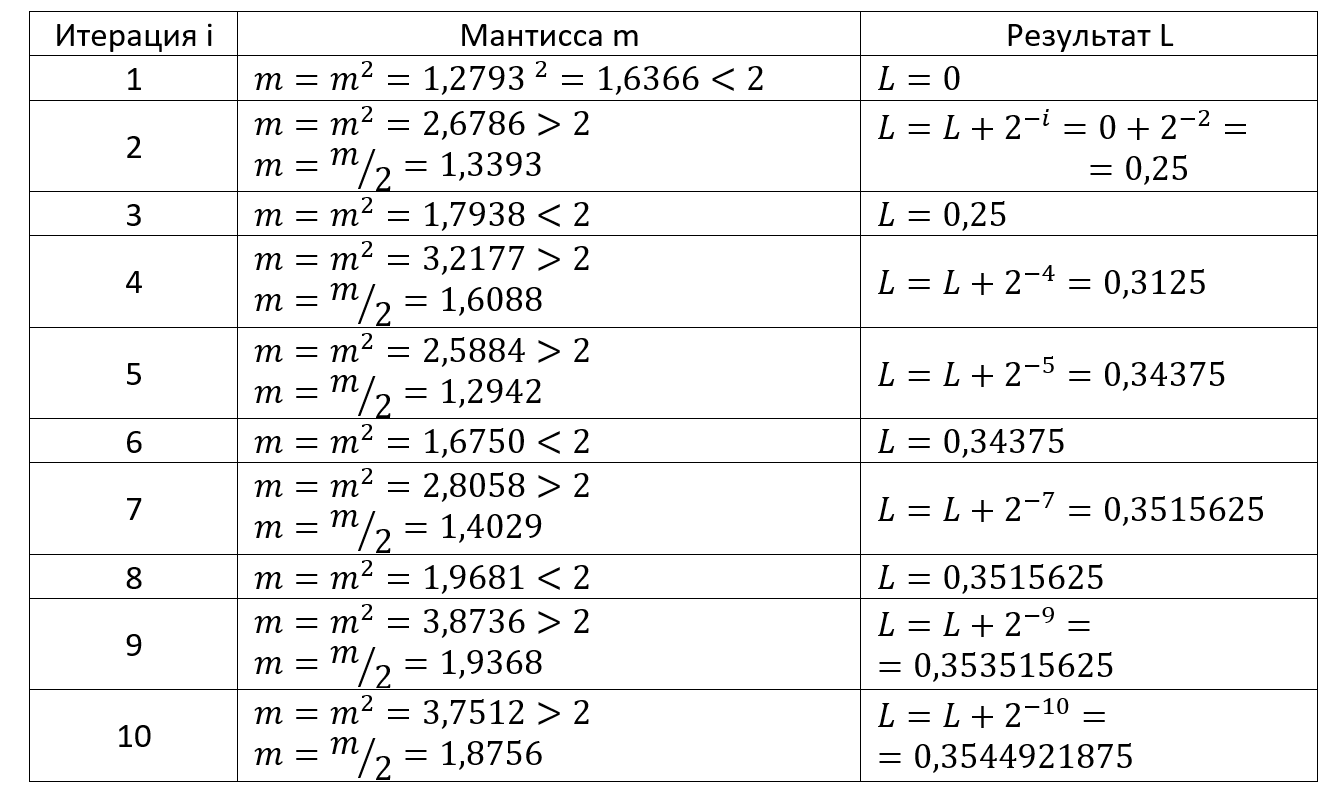
L=log_2m=0,3544921875.
3. Сумма
Результатом log2(X) итерационным методом является сумма экспоненты e и L
Y = log2X = e + L = 3+ 0,3544921875 = 3,3544921875
Погрешность err = |log2Xtrue - log2Xapprox | = 0,000886, но про нее будет далее.
Пример №2
Дано:
Входное значение X = 0,0666
Точность (разрядность дробной части) – 12 бит.
Решение:
1. Вычисление e и m
Поскольку X < 1, значит производится умножение. e = 0.
Цикл:

Экспонента e = -4.
Мантисса m = 1,0656.
2. Логарифмическое преобразование
Цикл из 12 итераций. L = 0.

L=log2m=0,091552734375.
3. Сумма
Результатом log2(X) есть сумма экспоненты e и L
Y = log2X = e + L = -4 + 0,091552734375 = -3,908447265625
Погрешность err= |log2Xtrue - log2Xapprox | = 0,000113, но про нее будет далее.
Реализация
На основе представленного итерационного алгоритма разработан RTL-блок log2Calc.vhd и тестовый стенд tb_log2Calc на языке VHDL. Параметры и порты описаны в таблицах 1 и 2.
Таблица 1 – Входные параметры блока log2Calc.vhd
| Название |
Тип |
Описание |
| DW_IN |
natural |
Разрядность входного вектора данных |
| DW_IN_FRAC |
natural |
Разрядность дробной части входного вектора данных, она же точность |
| DW_OUT |
natural |
Разрядность выходного вектора данных |
| DW_OUT_FRAC |
natural |
Разрядность дробной части выходного вектора данных, она же точность |
Параметры DW_IN, DW_IN_FRAC и DW_OUT_FRAC задаются пользователем, а разрядность выходного вектора DW_OUT задается функцией calc_dw из log2Calc_pkg на основе указанные выше трех параметров. RTL-блок не работает в конвейерном режиме, т.е. для вычисления одного значения требуется некоторое количество тактов, которое определяется функцией calc_latency из log2Calc_pkg.
Таблица 2 – Входные и выходные порты блока log2Calc.vhd
| Название |
Тип |
Направление |
Описание |
| clk |
std_logic |
Вход |
Тактовый сигнал |
| rst |
std_logic |
Вход |
Асинхронный сброс |
| valid_i |
std_logic |
Вход |
Сигнал готовности входных данных |
| data_i |
std_logic_vector
(DW_IN - 1 downto 0)
|
Вход |
Входные данные |
| rdy_o |
std_logic |
Выход |
Сигнал готовности приема входных данных |
| valid_o |
std_logic |
Выход |
Сигнал готовности выходных данных |
| data_o |
std_logic_vector
(DW_OUT - 1 downto 0)
|
Выход |
Выходные данные |
В тестовом стенде в соответствии со структурной схемой на рисунке 4 выполняются два процесса:
- процесс input_proc выполняет формирование входных данных на тестируемый блок с полным перебором входных значений Xstd;
- процесс output_proc получает выходные данные Ystd из тестируемого блока и эталонное значение Yin, вычисляет погрешность.
Точность вычисления оценивается на основе:
errabs = |Yin - Yout |
- относительная погрешность
errrel = |Yin - Yout | / Yin
- относительная погрешность в дБ
errrel_dB=20∙log10(|Yin - Yout | / Yin ),
где Yin – ожидаемый результат в формате real, Yout – вычисленный результат в формате real, полученный из вектора Ystd.
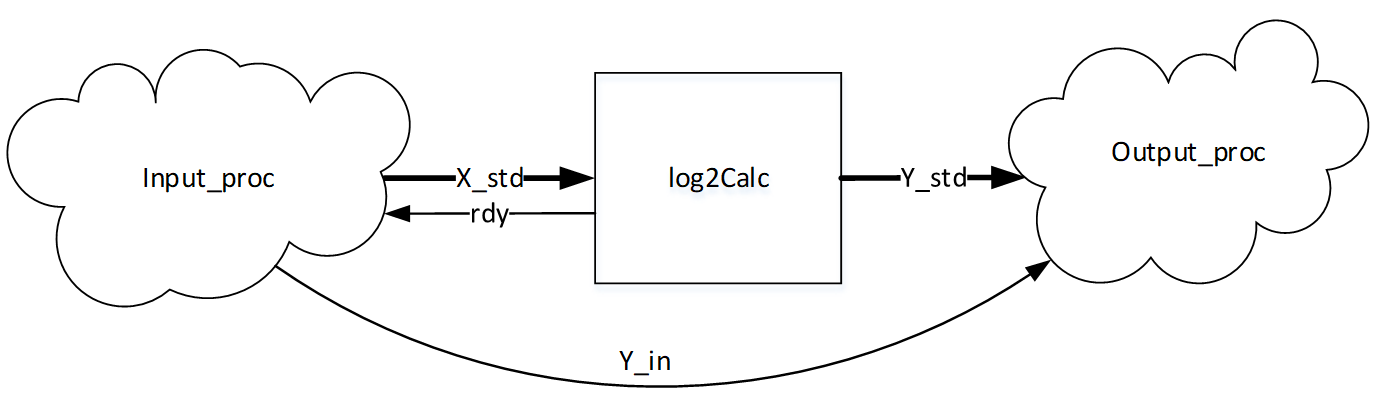
Рисунок 4 – Структурная схема тестового стенда
Пример №3
DW_IN = 12, DW_IN_FRAC = 10, DW_OUT_FRAC = 14, что соответствует формату входных данных ufix12_10 и выходных fixX_14.
На рисунке 5 изображен результат вычисления RTL-блоком log2Calc.vhd, который представляет собой график Y = log2(X). Поскольку входные данные представлены в формате ufix12_10, то они принимают значения от 0 до 4 с точностью 2-10.
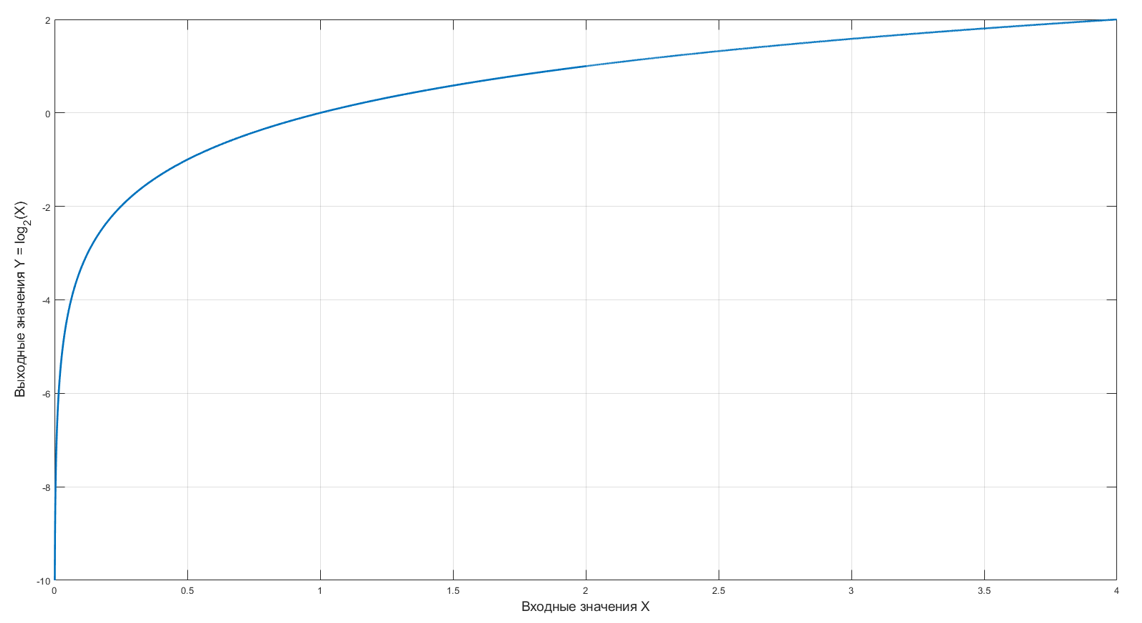
Рисунок 5 – График вычисленной функции Y = log2(X)
На рисунке 6 изображены графики трех видов рассматриваемых погрешностей. Наиболее информативной является относительная погрешность в дБ, на основе ее и будет оцениваться точность RTL-блока. Как видно из графика (см. рисунок 7) погрешность вычисления значительно возрастает в близи входного значения X = 1. Это объясняется тем, что log2(~1)=~0, т.е. возрастает отношение погрешности |Yin-Yout | к ожидаемому значению Yin из-за того, что погрешность в целом постоянная (см. первый график на рисунке 6), а Yin мала. Максимальная относительная погрешность на рисунке 7 составляет -27,2 дБ в окрестности входного значения Х = 1.
Помимо этого, наблюдается возрастание погрешности при входных значениях больше Х > 2. Это объявляется тем, что при X > 2 начинает отрабатывать вычисление экспоненты и, вероятно, это вычисление вносит свою дополнительную погрешность.
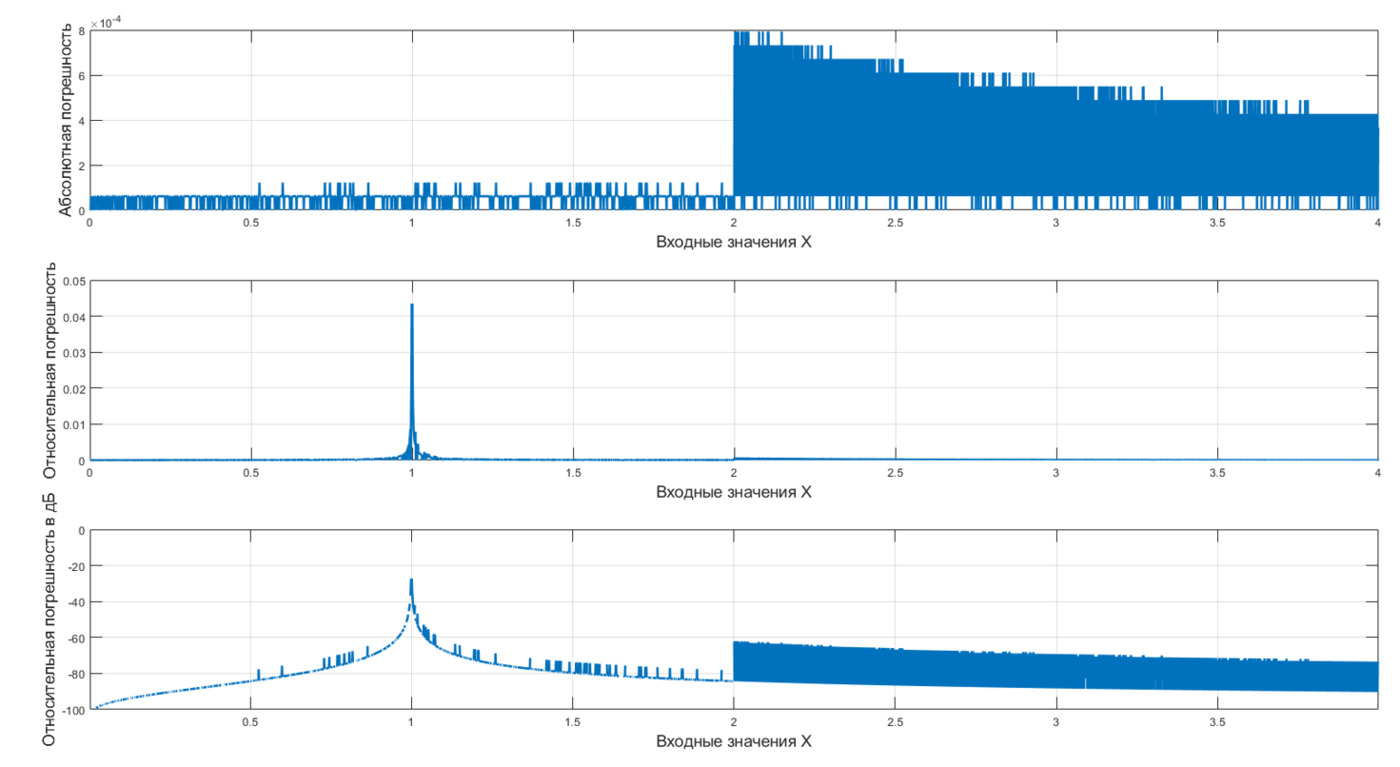
Рисунок 6 – График абсолютной, относительной и относительной в дБ погрешности
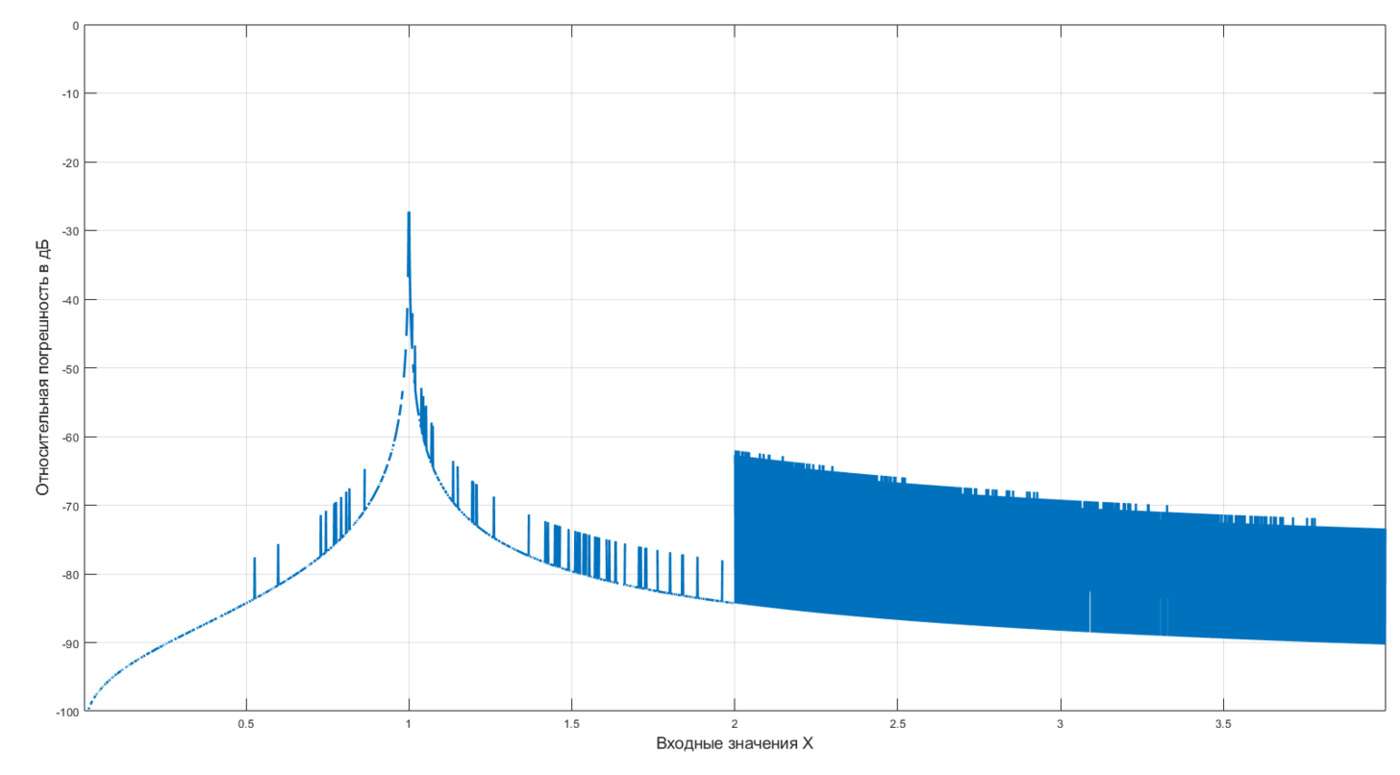
Рисунок 7 – График относительной погрешности в дБ
Точность
Проведен сравнительный анализ погрешности при разной точности входных и выходных данных, результаты представлены в таблице 3. Из таблицы можно сделать вывод, что сравнительно малая погрешность (-27 дБ) обеспечивается, когда точность выхода больше точности входа минимум на 4 разряда. Помимо этого, не рекомендуется устанавливать входную точность менее 10 разрядов.
Таблица 3 – Сравнение относительной погрешности (дБ) при разной точности входных и выходных данных
| Формат выходных данных |
|
Формат входных данных |
| ufix12_10 |
ufix14_12 |
ufix16_14 |
| fixX_10 |
0* |
-** |
- |
| fixX_12 |
-15,5 |
0 |
- |
| fixX_14 |
-27,2 |
-15,6 |
0 |
| fixX_16 |
-39,3 |
-27,2 |
-15,6 |
| fixX_18 |
-51,3 |
-39,3 |
-27,2 |
| fixX_20 |
-63,1 |
-51,3 |
-39,3 |
| fixX_22 |
-63,1 |
-63,4 |
-51,3 |
(*) – 0 дБ означает, что амплитуда абсолютной погрешности равна или сопоставима с амплитудой вычисленного значения
(**) – абсолютная погрешность больше вычисленного значения, не рабочая конфигурация
Ресурсоемкость
Ресурсоемкость RTL-блока в зависимости от параметров представлена ниже в таблицах 4. Сравнение проводилось на ПЛИС Xilinx Artix-7 в среде разработки Vivado 2018.3. RTL-блок не использует блочную память BRAM. Из приведенных результатов ресурсоемкости можно заметить, что при точности выходных данных более 20 бит снижается количество требуемых LUT и добавляется одно DSP48E1. Это объясняется тем, что некоторые операций на LUT при возросшей разрядности синтезатор считает, что оптимальнее выполнять на DSP48E1.
Таблица 4 – Сравнение ресурсоемкости
| |
Формат входных данных |
| Формат выходных данных |
ufix12_10 |
ufix14_12 |
ufix16_14 |
| LUT |
FF |
DSP |
LUT |
FF |
DSP |
LUT |
FF |
DSP |
| fixX_10 |
102 |
90 |
1 |
110 |
94 |
1 |
118 |
98 |
1 |
| fixX_12 |
108 |
96 |
1 |
116 |
98 |
1 |
122 |
102 |
1 |
| fixX_14 |
112 |
100 |
1 |
117 |
102 |
1 |
123 |
104 |
1 |
| fixX_16 |
122 |
109 |
1 |
128 |
111 |
1 |
133 |
113 |
1 |
| fixX_18 |
185 |
115 |
1 |
190 |
117 |
1 |
194 |
119 |
1 |
| fixX_20 |
136 |
121 |
2 |
135 |
123 |
2 |
142 |
125 |
2 |
| fixX_22 |
141 |
127 |
2 |
145 |
129 |
2 |
151 |
131 |
2 |
Вывод
Представленный RTL-блок вычисления двоичного логарифма в формате точности с фиксированной точкой допустимо применять в разработке ПО под ПЛИС. Рекомендуется, чтобы точность выходных данных была больше входных минимум на 4 разряда. RTL-блок является кроссплатформенным.
Литература
[1] A New Hardware Implementation of Base 2 Logarithm for FPGA - A.M.Mansour - 2015
Код модуля и тестбенч
Код модуля
----====================================================================================================================
----=========== PKG
----====================================================================================================================
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;
use ieee.math_real.all;
package log2Calc_pkg is
-- расчет выходной разрядности
function calc_dw(
dw_in : natural;
dw_in_frac : natural;
dw_out_frac : natural
) return natural;
-- определение задержки
function calc_latency(
dw_out : natural;
dw_out_frac : natural
) return natural;
end package log2Calc_pkg;
package body log2Calc_pkg is
----------------------------------------------------------------
-- расчет выходной разрядности
----------------------------------------------------------------
function calc_dw(
dw_in : natural;
dw_in_frac : natural;
dw_out_frac : natural
) return natural is
variable dw_in_int : natural;
variable dw_out_int : natural;
variable value : natural;
begin
dw_in_int := dw_in - dw_in_frac;
if (dw_in_int >= dw_in_frac) then
dw_out_int := natural(ceil(log2(real(dw_in_int))));
else
dw_out_int := natural(ceil(log2(real(dw_in_frac))));
end if;
value := dw_out_int + 1 + dw_out_frac;
return value;
end function calc_dw;
----------------------------------------------------------------
-- определение задержки
----------------------------------------------------------------
function calc_latency(
dw_out : natural;
dw_out_frac : natural
) return natural is
variable dw_out_int : natural;
variable value : natural;
begin
dw_out_int := dw_out - dw_out_frac;
value := 2 ** (dw_out_int - 1) + (dw_out_frac + 1) + 2;
return value;
end function calc_latency;
end package body log2Calc_pkg;
----====================================================================================================================
----=========== ENTITY
----====================================================================================================================
LIBRARY ieee;
USE ieee.std_logic_1164.all;
USE ieee.numeric_std.all;
use work.log2Calc_pkg.all;
ENTITY log2Calc IS
generic(
DW_IN : natural := 16;
DW_IN_FRAC : natural := 14;
DW_OUT_FRAC : natural := 22;
DW_OUT : natural := work.log2Calc_pkg.calc_dw(16, 14, 22)
);
PORT(
clk : in std_logic;
rst : in std_logic;
valid_i : in std_logic;
data_i : in std_logic_vector(DW_IN - 1 downto 0); -- unsigned
rdy_o : out std_logic;
valid_o : out std_logic;
data_o : out std_logic_vector(DW_OUT - 1 downto 0) -- signed
);
END log2Calc;
ARCHITECTURE rtl OF log2Calc IS
constant DW_IN_INT : natural := DW_IN - DW_IN_FRAC;
constant DW_OUT_INT : natural := DW_OUT - DW_OUT_FRAC;
type state_t is (IDLE,
EXPONENT,
MANTISSA,
RESULT
);
signal STATE : state_t;
signal zero : std_logic;
signal order : boolean; -- true - [1,..) / false - (0, 1)
constant LEN_CNT_EXP : natural := 2 ** (DW_OUT_INT - 1) + 1;
signal cnt_exp : integer range 0 to LEN_CNT_EXP - 1;
signal buf : integer range 0 to LEN_CNT_EXP - 1;
constant STD_1 : unsigned(DW_IN downto 0) := to_unsigned(integer(1.0 * real(2 ** DW_IN_FRAC)), DW_IN + 1); -- ровно 1
constant STD_2 : unsigned(DW_IN downto 0) := to_unsigned(integer(2.0 * real(2 ** DW_IN_FRAC)), DW_IN + 1); -- ровно 2
signal shift : unsigned(DW_IN downto 0);
signal exp_rdy : std_logic;
signal exp_sh : signed(DW_OUT - 1 downto 0); -- значение целой части без дробной
signal exp : signed(DW_OUT - 1 downto 0); -- значение целой части с учетом выделения бит под дробную (дробная по нулям)
function max_nat(a : natural;
b : natural
)
return natural is
begin
if (a > b) then
return a;
else
return b;
end if;
end function max_nat;
constant DW_NORM_FRAC : natural := max_nat(DW_IN_FRAC, DW_OUT_FRAC);
constant DW_NORM : natural := DW_NORM_FRAC + 2; -- [0,4)
signal norm : unsigned(DW_NORM - 1 downto 0);
constant STD2_NORM : unsigned(DW_NORM - 1 downto 0) := to_unsigned(integer(2.0 * real(2 ** DW_NORM_FRAC)), DW_NORM); -- ровно 2
signal cnt_mant : integer range 0 to DW_OUT_FRAC;
signal mant : std_logic_vector(DW_OUT - 1 downto 0);
begin
log2_proc : process(clk, rst)
variable shift2_v : unsigned(DW_NORM - 1 downto 0);
variable mult2_v : unsigned(2 * DW_NORM - 1 downto 0);
begin
if (rst = '1') then
STATE <= IDLE;
zero <= '0';
order <= true;
cnt_exp <= 0;
buf <= 0;
exp_rdy <= '0';
exp_sh <= (others => '0');
exp <= (others => '0');
shift <= (others => '0');
norm <= (others => '0');
cnt_mant <= 0;
mant <= (others => '0');
rdy_o <= '0';
valid_o <= '0';
data_o <= (others => '0');
elsif rising_edge(clk) then
case STATE is
--====================================================================================================================
--=========== ожидание, определение больше 1 или нет
--====================================================================================================================
when IDLE =>
valid_o <= '0';
if (valid_i = '1') then
if (unsigned(data_i) = 0) then
zero <= '1';
else
zero <= '0';
end if;
rdy_o <= '0';
buf <= 0;
cnt_exp <= 1;
shift <= unsigned('0' & data_i);
exp_rdy <= '0';
exp_sh <= (others => '0');
norm <= (others => '0');
cnt_mant <= 0;
mant <= (others => '0');
if (unsigned('0' & data_i) < STD_1) then -- в диапазоне (0,1)
order <= false;
else -- в диапазоне [1,..)
order <= true;
end if;
STATE <= EXPONENT;
else
rdy_o <= '1';
end if;
--====================================================================================================================
--=========== вычисление целой части
--====================================================================================================================
when EXPONENT =>
if (cnt_exp = LEN_CNT_EXP - 1) then
cnt_exp <= 0;
STATE <= MANTISSA;
else
cnt_exp <= cnt_exp + 1;
end if;
buf <= cnt_exp;
if (order) then -- больше 1 [1,..)
-- смещаем вправо (делим на 2) до тех пор, пока не будет меньше 2
shift <= shift_right(shift, 1); -- /2
if (shift <= STD_2 and exp_rdy = '0') then
exp_rdy <= '1';
exp_sh <= resize(to_signed(buf, DW_OUT_INT), DW_OUT);
if (DW_IN_FRAC = DW_NORM_FRAC) then
norm <= unsigned(shift((DW_IN_FRAC + 2) - 1 downto 0));
else
norm(DW_NORM - 1 downto DW_NORM - (DW_IN_FRAC + 2)) <= unsigned(shift((DW_IN_FRAC + 2) - 1 downto 0));
norm(DW_NORM - (DW_IN_FRAC + 2) - 1 downto 0) <= (others => '0');
end if;
end if;
else -- меньше 1 (0, 1)
-- смещаем влево (умножаем на 2) до тех порт, пока не будет больше 1
shift <= shift_left(shift, 1); -- *2
if (shift >= STD_1 and exp_rdy = '0') then
exp_rdy <= '1';
exp_sh <= resize(-to_signed(buf, DW_OUT_INT), DW_OUT);
if (DW_IN_FRAC = DW_NORM_FRAC) then
norm <= unsigned(shift((DW_IN_FRAC + 2) - 1 downto 0));
else
norm(DW_NORM - 1 downto DW_NORM - (DW_IN_FRAC + 2)) <= unsigned(shift((DW_IN_FRAC + 2) - 1 downto 0));
norm(DW_NORM - (DW_IN_FRAC + 2) - 1 downto 0) <= (others => '0');
end if;
end if;
end if;
--====================================================================================================================
--=========== вычисление дробной части
--====================================================================================================================
when MANTISSA =>
if (cnt_mant = DW_OUT_FRAC) then
cnt_mant <= 0;
-- overflow
if (exp_rdy = '1') then
exp <= shift_left(exp_sh, DW_OUT_FRAC);
else
exp <= to_signed(integer(-(DW_IN_INT - 1) * 2 ** (DW_OUT_FRAC)), DW_OUT);
end if;
rdy_o <= '1';
STATE <= RESULT;
else
cnt_mant <= cnt_mant + 1;
end if;
if (norm >= STD2_NORM) then
mant(DW_OUT_FRAC - cnt_mant) <= '1';
shift2_v := shift_right(norm, 1);
mult2_v := shift2_v * shift2_v;
else
mult2_v := norm * norm;
end if;
norm <= unsigned(mult2_v(DW_NORM - 1 + DW_NORM_FRAC downto DW_NORM_FRAC));
--====================================================================================================================
--=========== суммирование целой и дробной частей
--====================================================================================================================
when RESULT =>
valid_o <= '1';
if (zero = '1') then -- если вход нуль, то выдаем минимально возможное значение
data_o(DW_OUT - 1) <= '1';
data_o(DW_OUT - 2 downto 0) <= (others => '0');
else
data_o <= std_logic_vector(exp + signed(mant));
end if;
exp_rdy <= '0';
exp_sh <= (others => '0');
norm <= (others => '0');
mant <= (others => '0');
STATE <= IDLE;
end case;
end if;
end process;
END rtl;
|
Тестбенч
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
USE IEEE.NUMERIC_STD.all;
use ieee.math_real.all;
use std.textio.all;
use std.env.all;
entity tb_log2Calc is
generic(
DW_IN : natural := 12;
DW_IN_FRAC : natural := 10;
DW_OUT_FRAC : natural := 10
);
end entity;
architecture beh of tb_log2Calc is
procedure clk_wait(
signal clk : in std_logic;
constant th : integer
) is
begin
for i in 0 to th - 1 loop
wait until rising_edge(clk);
end loop;
end procedure clk_wait;
-- переводит число типа real в std_logic_vector длины dw и точности dw_frac
function real2std(data : real;
dw : integer;
dw_frac : integer;
sign : boolean
) return std_logic_vector is
begin
if (sign) then
return std_logic_vector(to_signed(integer(data * real(2 ** dw_frac)), dw));
else
return std_logic_vector(to_unsigned(integer(data * real(2 ** dw_frac)), dw));
end if;
end;
-- переводит число типа std_logic_vector длины dw и точности dw_frac в real
function std2real(data : std_logic_vector;
dw_frac : integer;
sign : boolean
) return real is
begin
if (sign) then
return real(to_integer(signed(data))) / real(2 ** dw_frac);
else
return real(to_integer(unsigned(data))) / real(2 ** dw_frac);
end if;
end;
--====================================================================================================================
--=========== вычисление целой части y = log2(x)
--====================================================================================================================
constant DW_IN_INT : natural := DW_IN - DW_IN_FRAC; -- разрядность целой части входных даннных
constant DW_OUT : natural := work.log2Calc_pkg.calc_dw(DW_IN, DW_IN_FRAC, DW_OUT_FRAC); -- разрядность выходных данных
constant LATENCY : natural := work.log2Calc_pkg.calc_latency(DW_OUT, DW_OUT_FRAC); -- вычислительная задержка блока
--====================================================================================================================
--=========== сигналы
--====================================================================================================================
constant PERIOD : time := 10 us;
signal clk : std_logic := '0';
signal rst : std_logic := '1';
signal en : std_logic;
-- signal cnt : integer range 0 to NUM_DATA - 1;
signal y_in : real := 0.0;
signal y_in_std : std_logic_vector(DW_OUT - 1 downto 0) := (others => '0');
signal x_valid : std_logic := '0';
signal x_std : std_logic_vector(DW_IN - 1 downto 0) := (others => '0');
constant ONES : std_logic_vector(DW_IN - 1 downto 0) := (others => '1');
signal x : real := 0.0;
signal rdy_o : std_logic;
signal rdy_z : std_logic;
signal y_out_valid : std_logic;
signal y_out_std : std_logic_vector(DW_OUT - 1 downto 0);
signal y_out : real := 0.0;
constant DW_ERR : natural := 32;
constant DW_ERR_FRAC : natural := 20;
signal err_abs : real := 0.0;
signal err_relative : real := 0.0;
signal err_relative_dB : real := 0.0;
signal err_abs_std : std_logic_vector(DW_ERR - 1 downto 0) := (others => '0');
signal err_relative_std : std_logic_vector(DW_ERR - 1 downto 0) := (others => '0');
signal err_relative_dB_std : std_logic_vector(DW_ERR - 1 downto 0) := (others => '0');
begin
-- clk, rst
proc_clk : process
begin
wait for PERIOD / 2;
clk <= not clk;
end process;
proc_rst : process
begin
rst <= '1';
wait for 15.2 * PERIOD;
rst <= '0';
wait;
end process;
--====================================================================================================================
--=========== формирование данных на блок
--====================================================================================================================
input_proc : process(clk, rst)
begin
if (rst = '1') then
en <= '1';
x_valid <= '0';
x_std <= (others => '0');
elsif rising_edge(clk) then
rdy_z <= rdy_o;
if (en = '1') then
if (rdy_z = '0' and rdy_o = '1') then
if (x_std = ONES) then
en <= '0';
x_valid <= '0';
else
x_std <= std_logic_vector(unsigned(x_std) + 1);
x_valid <= '1';
end if;
else
x_valid <= '0';
end if;
end if;
y_in <= log2(x);
end if;
end process;
x <= std2real(x_std, DW_IN_FRAC, false);
y_in_std <= real2std(y_in, DW_OUT, DW_OUT_FRAC, false);
--====================================================================================================================
--=========== тестируемый блок
--====================================================================================================================
inst_log2 : entity work.log2Calc
generic map(
DW_IN => DW_IN,
DW_IN_FRAC => DW_IN_FRAC,
DW_OUT_FRAC => DW_OUT_FRAC,
DW_OUT => DW_OUT
)
port map(
clk => clk,
rst => rst,
valid_i => x_valid,
data_i => x_std,
rdy_o => rdy_o,
valid_o => y_out_valid,
data_o => y_out_std
);
--====================================================================================================================
--=========== сравнение вычисленного с ожидаемым, вывод погрешности вычисления
--====================================================================================================================
y_out <= std2real(y_out_std, DW_OUT_FRAC, true);
output_proc : process(clk, rst) is
variable err_abs_v : real;
variable err_rel_v : real;
variable err_rel_dB_v : real;
begin
if (rst = '1') then
elsif rising_edge(clk) then
err_abs_v := y_in - y_out;
if (y_in = 0.0) then
err_rel_v := 0.0;
else
err_rel_v := abs (err_abs_v / y_in);
end if;
err_rel_dB_v := 20.0 * log10(err_rel_v);
if (y_out_valid = '1') then
err_abs <= err_abs_v;
err_relative <= err_rel_v;
err_relative_dB <= err_rel_dB_v;
err_abs_std <= real2std(err_abs_v, DW_ERR, DW_ERR_FRAC, true);
err_relative_std <= real2std(err_rel_v, DW_ERR, DW_ERR_FRAC, true);
if (err_rel_v = 0.0) then
err_relative_dB_std <= err_relative_dB_std;
else
err_relative_dB_std <= real2std(err_rel_dB_v, DW_ERR, DW_ERR_FRAC, true);
end if;
end if;
end if;
end process output_proc;
proc_check_end : process is
begin
wait until (x_std = ONES and en = '0');
clk_wait(clk, 200);
report "END SIM" severity note;
finish(0);
end process proc_check_end;
end architecture;
|