Поточное вычисление двоичного логарифма

Главная » Статьи » Разное » Познавательное

В статье рассматриваются варианты реализации поточного вычисления двоичного логарифма, приводятся результаты измерения точности и ресурсоёмкости для ПЛИС Artix-7 и синтезатора Vivado 2020.2.

Было протестировано 3 алгоритма вычисления log₂(x) с некоторыми вариациями:

1. Алгоритм с линейной интерполяцией дробной части;
2. Табличный алгоритм без интерполяции промежуточных значений и с интерполяцией;
3. Алгоритм CORDIC в вариантах без повторения шагов, с двойным повторением и с частичным повторением.

Обзор

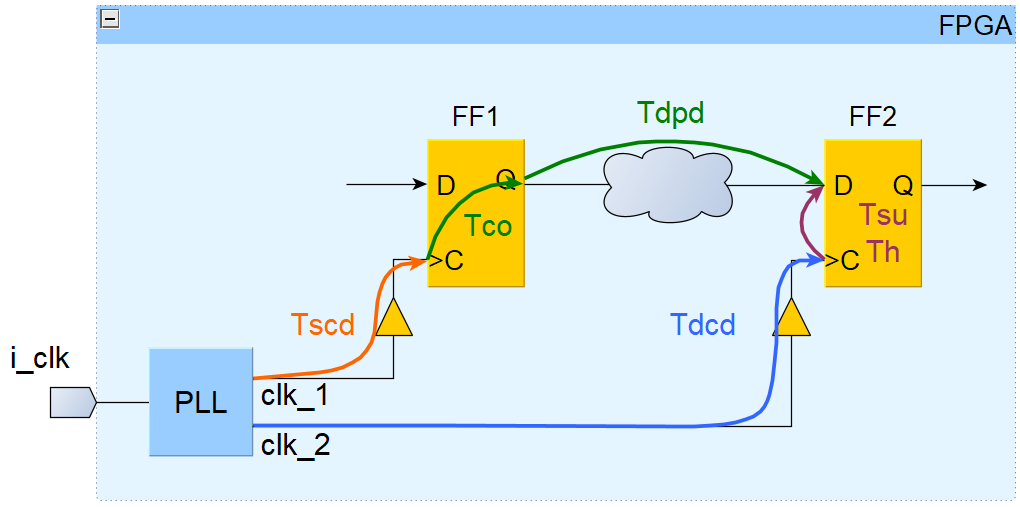
Все алгоритмы основаны на том, что log₂(x * 2^n) = log₂(x) + n. Т.е. задача вычисления двоичного логарифма сводится к приведению агрумента к интервалу [1..2) (нормализация) умножением/делением на 2 или двоичным сдвигом, и вычислении дробной части. Целой частью логарифма будет количество умножений/делений (сдвигов), необходимых для нормализации. Алгоритмы, показанные в статье, выполняют вычисление дробной части.

Нормализация агрумента

Алгоритм нормализации одинаков для всех вариантов вычисления логарифма и реализован в виде операции логарифмического сдвига, что быстрее и менее ресурсоёмко наивного побитового сдвига или приоритетного шифратора.

Алгоритм нормализации 16-битного числа в псевдокоде:

n = 0;
if ((x & 16'b1111_1111_0000_0000) == 0) { x = x << 8; n = n + 8; }
if ((x & 16'b1111_0000_0000_0000) == 0) { x = x << 4; n = n + 4; }
if ((x & 16'b1100_0000_0000_0000) == 0) { x = x << 2; n = n + 2; }
if ((x & 16'b1000_0000_0000_0000) == 0) { x = x << 1; n = n + 1; }

На выходе получаем сдвинутое к левому краю число и количество битовых сдвигов.

Пример:

x = 16'b0000_0000_0101_0001
n = 0

Шаг 1:
b0000_0000_0101_0001 &
b1111_1111_0000_0000 =
b0000_0000_0000_0000 == 0

x = x << 8 = b0101_0001_0000_0000
n = n + 8 = 8

Шаг 2:
b0101_0001_0000_0000 &
b1111_0000_0000_0000 =
b0101_0000_0000_0000 != 0

Шаг 3:
b0101_0001_0000_0000 &
b1100_0000_0000_0000 =
b0100_0000_0000_0000 != 0

Шаг 4:
b0101_0001_0000_0000 &
b1000_0000_0000_0000 =
b0000_0000_0000_0000 == 0

x = x << 1 = b1010_0010_0000_0000
n = n + 1 = 9

Для получения целой части логарифма нужно вычесть число n+1 из количества бит целой части входного числа. Общий результат получается суммированием целой части и дробной.

Например, пусть число из примера выше представлено в формате Q4.12, т.е. 4 бита целой части, и 12 бит дробной. Разность 4-(n+1) равна -6. Прибавлением дробной части к -6 получим результат между -6 и -5.

Нормализованое число представлено в формате Q1.15. Т.к целая часть всегда равна единице, диапазон значений находится в интервале [1..2). Из значения дробной части числа вычисляется дробная часть логарифма.

Алгоритм с линейной интерполяцией дробной части

Это самый простой, но в то же время самый неточный алгоритм. Для вычисления логарифма просто берется дробная часть нормализованного числа и конкатенируется с целой частью логарифма.

Возьмём число из примера выше:

x = 16'b0000.0000_0101_0001

Его десятичное предствление и значение функции log₂(x):

x = 16'b0000.0000_0101_0001 ≈ 0.019775390625
log2(0.019775390625) ≈ -5.660149997

После нормализации получаем:

x = b1.010_0010_0000_0000
n = 9
e = 4-(9+1) = -6 = b11010

Соединяем e и дробную часть нормализованного x:

y = b11010.010_0010_0000_0000 = -5.734375

Как можно видеть, ошибка вычисления составила 0.0742 (из приведенных ниже таблиц будет видно, что эта ошибка близка к максимальной). При вычислении этим способом значения децибел (20 * log₁₀(x)) ошибка будет составлять примерно 0.45dB, что для некоторых применений вполне приемлемо (ниже будет показано, как можно улучшить точность этого метода в два раза).

Табличный алгоритм

В табличном способе дробная часть логарифма берется из заранее созданной таблицы значений log₂(x) в интервале [1..2). В ПЛИС таблица реализуется в виде ROM с адресацией по дробной части нормализованного числа. Разрядность ROM (длина таблицы) выбирается из требуемой точности вычислений.

Улучшить точность табличного алгоритма можно с помощью линейной интерполяции между точками табличных значений. Для этого берутся оставшиеся после адреса ROM биты дробной части нормализованного числа, и умножаются на коэффициент, равный разности следующего и текущего значений из таблицы. Т.к. в потоковой реализации мы не можем два раза прочитать значение из ROM, целесообразно создать еще одну ROM с предвычисленными значениями коэффициентов для каждой точки, т.к. иначе придется продублировать ROM со значениями log₂(x) и добавить сумматор.

Вот как это выглядит на примере (пусть разрядность ROM будет равна 6 битам):

x = 16'b0010.010110010010 = 2.34814453125
log2(x) = 1.231521211

x(norm) = b1.0010110010010000
             |    ||        |
             +----++--------+
              ROM      z
              addr

rom_addr = b001011 = 11
z = b.0010010000 = 0.140625
e = 4-(2+1) = 1

l = ROM_log2(11) = 0.2288186905
k = ROM_k(11) = ROM_log2(12) - ROM_log2(11) = 0.0191088229

log2(x) = e + l + k * z = 1.2315058687

Ошибка вычисления составила 0.00001534

Алгоритм CORDIC

Алгоритм основан на последовательном приближении агрумента функции log₂(x) к единице с одновременным пересчетом результата функции путем прибавления или вычитания заранее вычисленных значений log₂(x), соответствующих множителю агрумента. Чтобы не использовать умножение, в методе CORDIC применяется битовый сдвиг, который эквивалентен умножению/делению на 2.

В основе алгоритма следующая формула:

log(a * (1±k)) = log(a) + log(1±k) = y + log(1±k)

Алгоритм в псевдокоде выглядит так:

k = 0.5
e, x = normalize(a) // e - количество сдвигов, x - нормализованный аргумент

loop(STEPS)
{
  if (x >= 1) {
    x = x * (1-k)
    e = e - log2(1-k)
  }
  else {
    x = x * (1+k)
    e = e - log2(1+k)
  }

  k = k / 2
}

return e

Этот алгоритм можно оптимизировать. Т.к. x всегда больше единицы, можно сразу разделить его на два, а к e прибавить единицу. Можно заметить, что после этого x всегда будет меньше единицы. Т.е. за цикл можно вынести первую итерацию, и совместить это с предыдущим действием:

x = x/2 + x/4
y = y + 1 - log2(1+0.5)
k = 1/4

Этот код нужно вставить перед циклом. Такая оптимизация улучшает сходимость и позволяет избавиться от одного сложения.

При некоторых начальных значениях x недостаточно приближается к единице, из-за чего падает точность вычислений. Улучшить сходимость помогает повторное вычисление шага с тем же значением k. Это можно делать на каждом шаге, но, как будет показано далее, лучший результат даёт выборочное повторение шагов.

Результаты моделирования

При моделировании использовались следующие параметры:

Параметр
Входная разрядность	18
Длина дробной части на входе	16
Выходная разрядность	18
Длина дробной части на выходе	12

Для каждого метода приведены следующие графики:

1. График вычисленного и референсного значений лорагифма на интервале 0..4;
2. График вычисленного и референсного значений лорагифма на интервале 1..2;
3. График абсолютной ошибки на интервале 1..2 в логарифмическом масштабе.

Размер таблицы для табличного алгоритма и количество стадий для CORDIC выбраны таким образом, чтобы точности алгоритмов были близки.

Алгоритм с линейной интерполяцией дробной части

Параметр	Значение
Максимальная абсолютная ошибка	0.04332992
Значащих бит в дробной части (мин)	4.53
Значащих бит в дробной части (сред)	5.25
Максимальная ошибка вычисления dB:	0.260872 db

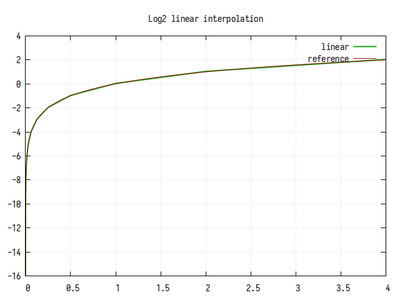
Рис.1: График log₂(x), вычисленного методом линейной интерполяции

На графике хорошо заметны линейные участки между степенями двойки по оси X.

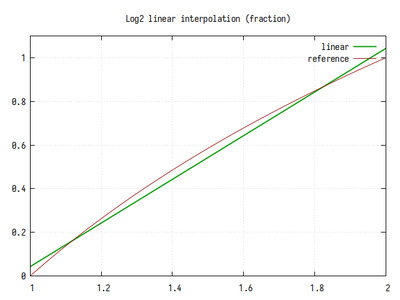
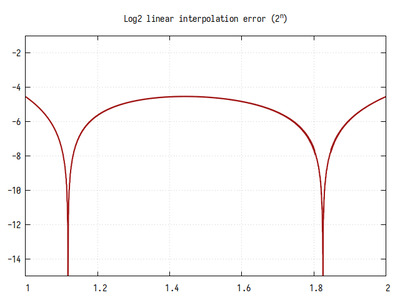
Рис.2: График log₂ на интервале 1..2

Как видно из графика, дробная часть логарифма представляет собой линейное приближение к референсному значению. В представленной реализации, для улучшения точности, к результирующему значению прибавляется константа 0.043. Это добавляет лишний сумматор, но улучшает точность в два раза.

Рис.3: Ошибка вычисления

В худшем случае точность вычисления составляет примерно 4.5 бита в дробной части, но в окрестностях точек пересечения прямой и log₂(x) (примерно 1.12 и 1.82) точность приближается к максимальной.

Табличный алгоритм без интерполяции

Размер таблицы - 256 элементов (разрядность 8 бит).

Параметр	Значение
Максимальная абсолютная ошибка	0.00292969
Значащих бит в дробной части (мин)	8.42
Значащих бит в дробной части (сред)	10.00
Максимальная ошибка вычисления dB:	0.017638 db

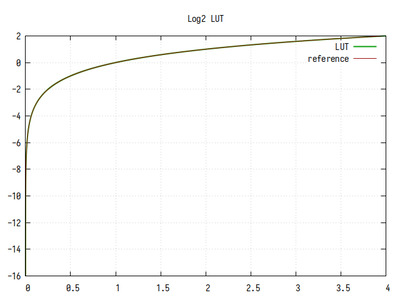
Рис.4: График log₂(x), вычисленного табличным методом без интерполяции

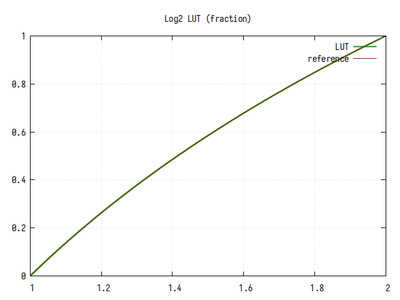
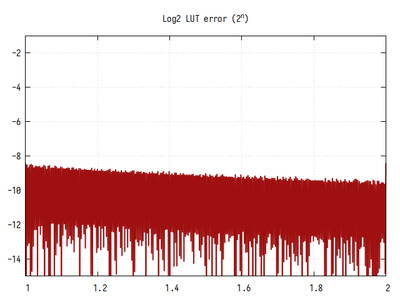
Рис.5: График log₂ на интервале 1..2

На общем графике погрешностей вычисления не заметно, однако на интервале 1..2 можно заметить ступеньки, возникающие из-за конечного размера таблицы подстановки.

Рис.6: Ошибка вычисления

Среднее количество значащих бит дробной части равно 10, и имеет небольшой спад в начале интервала, и подъем в конце. Это обусловлено разностью значений производной логарифма - в начале интервала она имеет большее значение, чем в конце, тогда как значения таблицы распределены равномерно. Если посмотреть на график ошибки на всех значениях X, то будет видно, что кривая повторяется на каждом интервале от 2^n до 2^(n+1).

Табличный алгоритм с интерполяцией

Размер таблицы - 8 элементов (разрядность 3 бита).

Параметр	Значение
Максимальная абсолютная ошибка	0.00274294
Значащих бит в дробной части (мин)	8.51
Значащих бит в дробной части (сред)	9.92
Максимальная ошибка вычисления dB:	0.016514 db

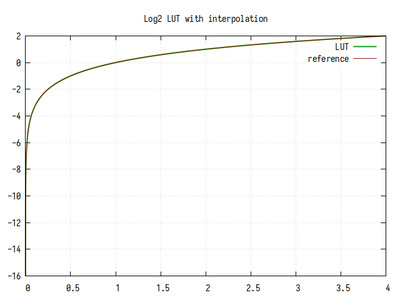
Рис.7: График log₂(x), вычисленного табличным методом с интерполяцией

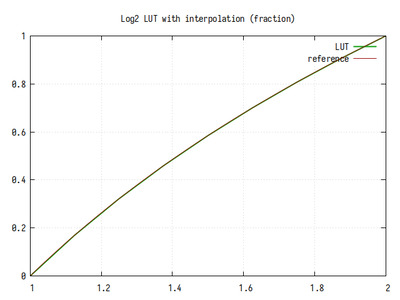
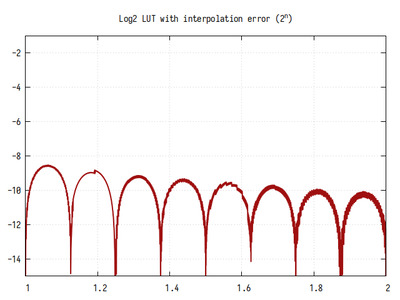
Рис.8: График log₂(x) на интервале 1..2

На интервале 1..2 едва заметны 8 линейных участков.

Рис.9: Ошибка вычисления

Среднее кол-во значащих бит дробной части около 10. Ошибка вычисления представляет собой произведение табличной ошибки и ошибки линейной интерполяции на 8 интервалах. На графике чётко видны 8 “колоколов”, как в алгоритме линейной интерполяции, а так же уменьшение ошибки с увеличением X, как в табличном без интерполяции. Небольшие флуктуации на графике обусловлены конечной разрядностью выходного кода.

Алгоритм CORDIC без дублирования шагов

Количество шагов - 12.

Параметр	Значение
Максимальная абсолютная ошибка	0.06852803
Значащих бит в дробной части (мин)	3.87
Значащих бит в дробной части (сред)	8.52
Максимальная ошибка вычисления dB:	0.412580 db

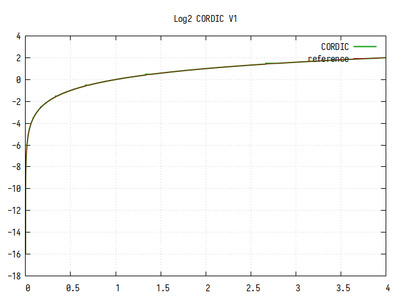
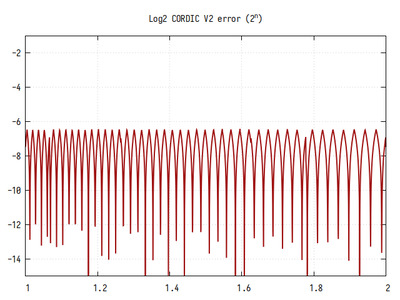
Рис.10: График log₂(x), вычисленного алгоритмом CORDIC

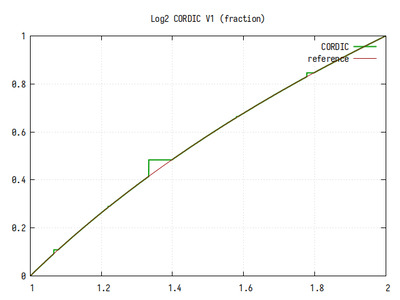
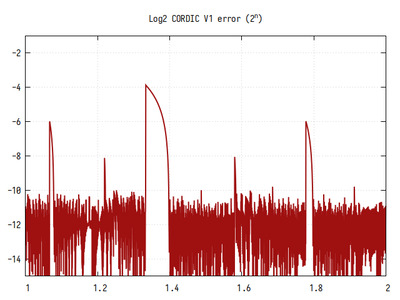
Рис.11: График log₂(x) на интервале 1..2

В целом, алгоритм CORDIC обеспечивает очень хорошее приближение к референсному значению, кроме участков плохой сходимости, которые видны на графиках в виде выбросов. Видно, что кроме больших участков плохой сходимости есть участки поменьше и еще меньше, что похоже на фрактальный рисунок.

Рис.12: Ошибка вычисления

Если бы не выбросы, точность вычисления логарифма была бы более 10 двоичных знаков в дробной части.

Алгоритм CORDIC с дублированием каждого шага

Количество шагов - 12, значение k повторяется по два раза.

Параметр	Значение
Максимальная абсолютная ошибка	0.01168009
Значащих бит в дробной части (мин)	6.42
Значащих бит в дробной части (сред)	7.48
Максимальная ошибка вычисления dB:	0.070321 db

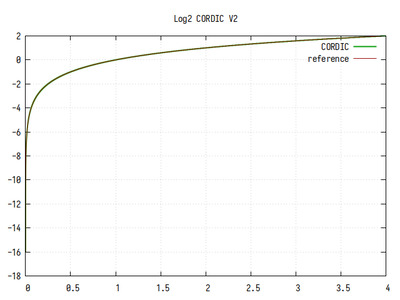
Рис.13: График log₂(x), вычисленного алгоритмом CORDIC с полным дублированием

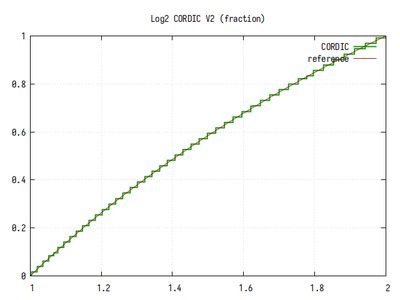
Рис.14: График log₂(x) на интервале 1..2

Из-за дублирования всех шагов, минимальный шаг приближения уменьшился в 64 раза (при 12 шагах всего, только на 6 шагах коэффициент k уменьшается в два раза), что сказалось на точности вычисления. Однако, выбросов, обусловленных плохой сходимостью не осталось.

Рис.15: Ошибка вычисления

Ошибка вычисления равномерная и постоянная, хоть и довольно высокая.

Алгоритм CORDIC с частичным дублированием

Количество шагов - 12, дублируются шаги 3, 5 и 7.

Параметр	Значение
Максимальная абсолютная ошибка	0.00211954
Значащих бит в дробной части (мин)	8.88
Значащих бит в дробной части (сред)	10.42
Максимальная ошибка вычисления dB:	0.012761 db

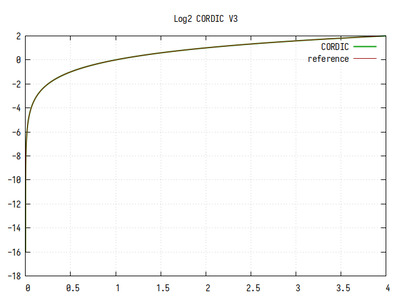
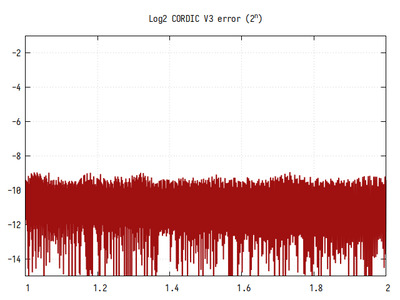
Рис.16: График log₂(x), вычисленного алгоритмом CORDIC с частичным дублированием

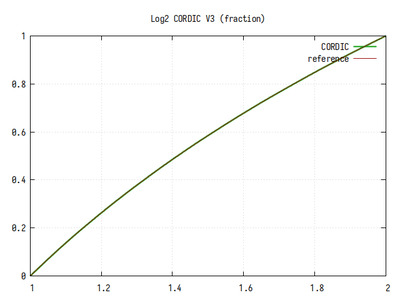
Рис.17: График log₂(x) на интервале 1..2

Если присмотреться, можно увидеть небольшие ступеньки на графике. Они меньше, чем в предыдущем варианте, но больше, чем в варианте без дублирования. Минимальный шаг приближения увеличился в 8 раз по сравнению с первым вариантом, но он меньше в 8 раз, чем во втором варианте.

Рис.18: Ошибка вычисления

Видно, что ошибка в целом равномерная и постоянная. Небольшие флуктуации появились из-за конечной разрядности выходного кода и из-за присутствия участков, где сходимость всё таки не полностью достигается. Тем не менее, среднее количество значащих бит около 10, и оно не зависит от аргумента.

Результаты синтеза

Синтез и трассировка проводились синтезатором Vivado 2020.2 для ПЛИС Artix-7a35 со стандартными настройками. Все варианты синтезировались с одинаковыми значениями ширины входного и выходного слова:

Параметр	Значение
Входная разрядность	18
Длина дробной части на входе	16
Выходная разрядность	18
Длина дробной части на выходе	12

Ниже представлены таблицы с результатами синтеза и моделирования.

Расшифровка названий строк в таблицах:

Название	Расшифровка
LUT	Количество LUT
FF	Количество триггеров
BRAM	Количество блоков памяти
DSP	Количество блоков DSP
FMAX	Максимальная частота клока (МГц)
Latency	Задержка между входным значением и результатом
Макс.ошибка	Максимальная абсолютная ошибка вычисления логарифма
SFB среднее	Среднее количество значащих бит дробной части

Алгоритм с линейной интерполяцией дробной части

Метод линейной интерполяции не имеет параметров и вариантов исполнения, по этому в таблице только один столбец.

LUT	69
FF	132
BRAM	-
DSP	-
FMAX	320
Latency	8
Макс.ошибка	0.043
SFB среднее	5.25

Комментировать здесь в общем нечего.

Табличный алгоритм без интерполяции

Был выполнен синтез нескольких вариантов модуля с разными размерами таблицы (указаны в шапке).

Размер таблицы:	64	128	256	512	1024	2048
LUT	62	77	101	153	62	64
FF	91	95	99	103	85	87
BRAM	-	-	-	-	0.5	1
DSP	-	-	-	-	-	-
FMAX	370	338	317	278	319	318
Latency	7	7	7	7	7	7
Макс.ошибка	0.011	0.0056	0.0029	0.0015	0.00079	0.00046
SFB среднее	8.00	9.00	10.00	10.98	11.96	12.85

Синтез табличного алгоритма сильно удивил тем, что таблицу до 512 элементов синтезатор реализовал в виде логики, при этом уместив всё в скромные 100-150 LUT. Кроме того, количество триггеров получилось заметно меньше, чем в алгоритме линейной интерполяцией.

Табличный алгоритм с интерполяцией

Размер таблицы:	8	16	32	64
LUT	86	91	89	98
FF	148	150	150	150
BRAM	-	-	-	-
DSP	1	1	1	1
FMAX	312	326	338	360
Latency	9	9	9	9
Макс.ошибка	0.0027	0.00093	0.00049	0.00046
SFB среднее	9.92	11.47	12.53	12.84

Табличный алгоритм с интерполяцией показал, пожалуй, лучший результат по соотношению ресурсы/точность, хоть и потребовал одного умножителя. При этом, в реализации есть возможность оптимизации для более полного использования ресурсов умножителя, что может уменьшить количество триггеров.

Алгоритм CORDIC без дублирования шагов

Для алгоритма CORDIC варьировалось количество шагов.

Итерации:	10	12	14
LUT	356	424	458
FF	416	490	546
BRAM	-	-	-
DSP	-	-	-
FMAX	320	300	328
Latency	16	18	20
Макс.ошибка	0.068	0.068	0.068
SFB среднее	8.27	8.52	8.55

Блок занимает в разы больше ресурсов, чем предыдущие варианты из-за большого количества стадий конвейера. Как было сказано ранее, просадка в точности в этом варианте происходит из-за плохой сходимости на некоторых значениях аргумента.

Алгоритм CORDIC с дублированием каждого шага

Итерации:	10	12	14
LUT	356	422	489
FF	417	491	565
BRAM	-	-	-
DSP	-	-	-
FMAX	329	287	304
Latency	16	18	20
Макс.ошибка	0.023	0.012	0.0062
SFB среднее	6.49	7.48	8.47

Количество ресурсов в этом варианте практически не изменилось, но точность выросла из-за хорошей сходимости.

Алгоритм CORDIC с дублированием в точках 3, 7, 11

Итерации:	6	8	10	12	14
LUT	225	291	358	423	490
FF	268	342	416	490	564
BRAM	-	-	-	-	-
DSP	-	-	-	-	-
FMAX	313	326	323	330	328
Latency	12	14	16	18	20
Макс.ошибка	0.049	0.0149	0.006	0.002	0.0014
SFB среднее	5.48	7.45	8.47	10.42	11.24

Этот вариант показал лучшую точность на всех значениях количества шагов.

Выводы

Самым эффективным с точки зрения ресурсов и скорости оказался табличный алгоритм с интерполяцией. А его вариант без интерполяции и с размером таблицы до 512 не нуждается в использовании BRAM или умножителя и показывает приемлемые результаты по точности.

Алгоритм линейной интерполяции, несмотря на его простоту, оказался не самым лучшим с точки зрения ресурсов. Однако, возможно показанную реализацию можно оптимизировать.

Из-за медленной сходимости приближения в алгоритме CORDIC необходимо увеличивать количество шагов приближения, что, с учётом потоковой реализации, требует большого количества ресурсов. Несмотря на это, итерационная реализация может показать хорошие результаты как по точности, так и по ресурсам. Кроме того, этот метод имеет самую равномерную ошибку вычисления, что может быть важно в некоторым случаях. Еще одно преимущество алгоритма в том, что он не использует умножители.

Приложение

Исходники: https://github.com/punzik/log2pipelined