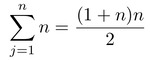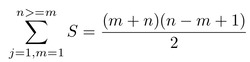К формальной проверке
Доказательство правильности работы устройства
Раздел програмных движков [engines]
Формальные испытания
Этот пример я буду строить на основе не противоречивого и давно доказанного высказывания, а именно на основе формулы для подсчёта суммы чисел натурального ряда. Эта всем известная со времён Пифагора (как заверяет википедия) формула утверждает следующее:
При ∀n ∈ ℕ истинность этого высказывания можно проверить простой подстановкой чисел и сравнением результата с простым суммированием. Очевидно, что результаты должны совпадать. Так же, это высказывание остаётся истинным и при ограничении суммы снизу.
Что можно проверить, если от суммы S(n) вычесть сумму S(m-1). В случае, если n = m суммой будет само число n. И это тоже верно, поскольку сумма чисел показывает сколько единиц находится в этой сумме. Удивительно, но высказывание работает и при отрицательных числах, но это уже не относится к натуральному ряду.
Вооружившись формулой на последнем рисунке мы перейдём к разработке модуля, который и будет рассчитывать сумму ряда натуральных чисел без 0, ограниченную числами n и m при n>=m.
Один из вариантов такого модуля представлен ниже.
module sum_n
(
input wire clk_in,
input wire [7:0] n_in, m_in,
output wire [15:0] s_out);
)
assign s_out = (m_in + n_in) * (n_in - m_in + 1) / 2;
endmodule
Вся формула записывается одним предложением assign и не требует последовательностной (секвенциальной) логики. Создадим стенд для испытания этого модуля.
`timescale 1ns/1ps
module sum_n_tb();
reg clk;
reg [7:0] A, B;
wire [15:0] S;
initial begin
#0 clk = 0;
forever #10 clk = ~clk;
end
sum_n inst_sum_n
(
.clk_in(clk),
.m_in(A),
.n_in(B),
.s_out(S)
);
initial begin
repeat(20)begin
B = $random;
A = $random;
@(posedge clk) begin
$monitor("A=%d B=%d S=%d",A,B,S);
end
end
$finish;
end
initial begin
$dumpfile("out.vcd");
$dumpvars(0, sum_n_tb);
end
endmodule // sum_n
Запустим стенд на исполнение и посмотрим на результаты работы модуля.
$ vvp a.out
VCD info: dumpfile out.vcd opened for output.
A= 99 B= 9 S=60730
A=141 B= 13 S=55757
A= 18 B=101 S= 4998
A= 13 B= 1 S=65459
A= 61 B=118 S= 5191
A=140 B=237 S=18473
A=198 B=249 S=11622
A=170 B=197 S= 5138
A=119 B=229 S=19314
sum_n_tb.v:32: $finish called at 190000 (1ps)
A=119 B=229 S=19314
Уже при беглом взгляде на этот результат видно, что в некоторых случаях сумма верна, а в некоторых случаях нет. Давайте разберёмся с тем, что происходит в не правильных случаях. Нетрудно заметить, что в этих случаях нарушается условие n ≥ m и мы получаем некую отрицательную сумму. Введём в стенд ограничение. Будем вести расчёт только для пар n≥m
initial begin
repeat(20)begin
B = $random;
A = $random;
if(B ≥ A)begin
@(posedge clk) begin
$monitor("A=%d B=%d S=%d",A,B,S);
end
end
end
$finish;
end
Теперь результат будет следующий:
$ vvp a.out
VCD info: dumpfile out.vcd opened for output.
A= 61 B=118 S= 5191, 0x1447
A=140 B=237 S=18473, 0x4829
A=198 B=249 S=11622, 0x2d66
A=170 B=197 S= 5138, 0x1412
A=119 B=229 S=19314, 0x4b72
sum_n_tb.v:32: $finish called at 110000 (1ps)
A=119 B=229 S=19314, 0x4b72
Проверим некоторые результаты, воспользовавшись листом бумаги и ручкой. У меня результаты совпали. Следовательно модуль работает правильно. Но давайте уточним. Правильнее можно сказать, что в этом модуле формула для расчёта суммы последовательности чисел натурального ряда при условии, что n ≥ m рассчитывает правильный результат. Большего о модуле пока сказать ничего нельзя.
Доказательство правильности работы устройства
Как можно проверить правильность работы этого устройства? Или, другими словами, как доказать истинность высказывания выраженного в модуле? Первое, что можно сделать это просто вычислить по известной формуле сумму и сравнить её с результатом, который выдаёт устройство. И, конечно, можно будет сразу увидеть правильно ли работает устройство или нет. И мы уже это сделали в предыдущем разделе. Но давайте посмотрим на эту проверку более тщательно. Такая проверка даст нам возможность убедиться только в том, что для конкретных, выбранных чисел результат верен. Но такая проверка не доказывает, что результат будет верен при всех возможных значениях.
Кроме того мы хотим доказать правильность работы самого устройства. А поскольку устройство состоит минимум из двух частей: устройство ввода и устройство вычисления, то и полная формула истинности будет включать в себя эти две части.
Давайте рассмотрим вопрос - с чем же мы будем работать строя доказательство?
Для этого посмотрим на текст, описывающий наш модуль. Этот текст эквивалентен самому устройству. Поэтому можно подвергнуть этот текст тщательному анализу на предмет вычленения из него утверждений, предположений и ограничений, записанных в тексте модуля. Из этих высказываний построим логическую формулу. Далее мы подвергнем логическому анализу полученную формулу и попытаемся доказать её истинность. Таков план, или путь.
Для доказательства истинности высказываний о работе модуля мы будем использовать программу sby (SymbiYosys). Эта программа-драйвер внешнего интерфейса для потоков формальной проверки оборудования на основе Yosys. Она является частью пакета САПР Tabby и пакета САПР OSS. Как только SBY установлен и доступен в командной строке как sby, его можно вызвать следующим образом.
usage: sby [options] [<jobname>.sby [tasknames] | <dirname>]
где
<jobname>.sby | <dirname>
файл .sby или каталог, содержащий файл config.sby
tasknames
задачи для выполнения (допустимы только при использовании <jobname>.sby)
Для получения более полной информации можно обратиться к странице руководства по SymbiYosys.
Здесь я коротко рассмотрю некоторые вещи.
Файл .sby состоит из разделов. Каждый раздел начинается с одной строки. заголовок раздела в квадратных скобках. Порядок разделов в .sby файле по большей части не имеет значения, но по соглашению обычный порядок таков [tasks], [options], [engines], [script], и [files].
Необязательный [tasks] раздел может использоваться для настройки нескольких задач проверки в одном .sby файле. Каждая строка в [tasks] разделе настраивает одну задачу. Например:
[tasks]
task1 task_1_or_2 task_1_or_3
task2 task_1_or_2
task3 task_1_or_3
Каждой задаче могут быть присвоены дополнительные групповые псевдонимы, такие как task_1_or_2 и task_1_or_3 в приведенном выше примере. Одна или несколько задач могут быть заданы в качестве дополнительных аргументов командной строки при вызове sby:
sby example.sby task2
Если задача не указана, то все задачи в [tasks] секции будут запущены.
После раздела [tasks] в разделе настроек [options] могут быть заданы отдельные строки для конкретной задачи или группы задач
[options]
task_1_or_2: mode bmc
task_1_or_2: depth 100
task3: mode prove
Если тег <taskname>: используется в строке сам по себе, тогда условная строка продолжается до следующего условного блока или -- на отдельной строчке.
[options]
task_1_or_2:
mode bmc
depth 100
task3:
mode prove
--
Метка ~<taskname>: может использоваться для строки или блока, которые не должны использоваться, когда данная задача активна:
[options]
~task3:
mode bmc
depth 100
task3:
mode prove
Раздел настроек [options]
Раздел настроек [options] содержит строки с парами ключ-значение. Параметр mode (режим) является обязательным. Возможными значениями для mode являются следующие варианты:
| Режим (mode) | Описание |
|---|---|
| bmc | Проверка ограниченной модели для проверки свойств безопасности ( assert(...) заявления |
| prove | Неограниченная проверка модели для проверки свойств безопасности ( assert(...) заявления) |
| live | Неограниченная проверка модели для проверки свойств живучести ( assert(s_eventually ...) заявления) |
| cover | Генерирует набор кратчайших трасс, необходимых для доступа ко всем операторам cover() |
Раздел програмных движков [engines]
В разделе [engines] настраивается, какие програмные движки следует использовать для решения данной проблемы. Каждая строка в [engines] указывает один програмный движок. Если указано более одного движка, то используется результат, возвращаемый первым програмным движком для завершения.
Каждая конфигурация движка состоит из названия програмного движка, за которым следуют настройки движка, обычно за ними следуют имя решателя и настройки решателя.
Пример:
[engines]
smtbmc --syn --nopresat z3 rewriter.cache_all=true opt.enable_sat=true
abc sim3 -W 15
В первой строке smtbmc это програмный движок, --syn --nopresat есть варианты програмного движка, z3 является решателем, и rewriter.cache_all=true opt.enable_sat=true являются вариантами решения.
Во 2-й строке abc есть програмный движок, вариантов движка нет, sim3 является решателем , и -W 15 есть варианты решения.
В настоящее время поддерживаются следующие комбинации режима / движка / решателя:
| Режим (mode) | Описание |
| bmc | smtbmc [all solvers] |
| btor btormc | |
| btor pono | |
| abc bmc3 | |
| abc sim3 | |
| aiger smtbmc | |
| prove | smtbmc [all solvers] |
| abc pdr | |
| aiger avy | |
| aiger suprove | |
| cover | smtbmc [all solvers] |
| btor btormc | |
| live | aiger suprove |
smtbmc програмный движок
Это странное сочетание букв в названии означает Satisfiability Modulo Theories (SMT) и Bounded Model Check (BMC) что можно перевести как Теории выполнимости по модулю (smt), Проверка ограниченной модели (bmc).
smtbmc движок работает в нескольких режимах (mode):
- bmc - ограниченная базовая проверка;
- prove - доказательство методом индукции;
- cover - расчёт покрытия.
btor
btor движок поддерживает аппаратные средства проверки моделей, которые принимают файлы btor2. Движок не поддерживает никаких настроек и поддерживает следующие решатели:
| Решатель | Режимы |
| btormc | bmc, cover |
| pono | bmc |
aiger движок
Движок aiger универсального интерфейсного оборудования modelcheckers. Обрабатывает файлы aiger. Им поддерживаются следующие решатели и режимы:
| Решатель | Режимы |
| suprove | prove, live |
| avy | prove |
| aigbmc | bmc |
abc движок
| Решатель | Режимы | Команда ABC |
| bmc3 | bmc | bmc3 -F <depth> -v |
| sim3 | bmc | sim3 -F <depth> -v |
| pdr | prove | pdr |
none движок
Движок none не запускает никакого решателя. Его можно использовать вместе с make_model параметром, что позволяет вручную создавать любые модели, поддерживаемые одним из прочих движков. Это упрощает использование той же модели за пределами sby.
Раздел скрипта [script]
Раздел [script] содержит сценарий Yosys, который читает и развивает дизайн тестируемого устройства. Например, для простого проекта в одном файле содержится дизайн mytest.sv с верхним модулем mytest:
[script]
read -sv mytest.sv
prep -top mytest
Или явно используя проверяемый анализатор SystemVerilog (по умолчанию для read -sv, когда Yosys собран с поддержкой Verific):
[script]
verific -sv mytest.sv
verific -import mytest
prep -top mytest
Или явно используя собственный анализатор Yosys Verilog (по умолчанию для read -sv когда Yosys не собран с поддержкой Verific):
[script]
read_verilog -sv mytest.sv
prep -top mytest
Исполните yosys в окне терминала и введите help в командной строке Yosys для получения списка команд. Запустите help <command> для получения подробного описания команды, например help prep.
Раздел файлов [files]
В разделе "Файлы" ([files]) перечисляются исходные файлы для проверки, что означает все файлы, к которым Yosys потребует доступ при чтении проекта, в том числе для файлов с примерами данных для $readmemh и $readmemb.
sby копирует эти файлы в <outdir>/src/ перед запуском скрипта Yosys. Когда скрипт Yosys будет выполнятся, он будет использовать копии в <outdir>/src/. (В качестве альтернативы, абсолютные имена файлов могут использоваться в скрипте Yosys для файлов, не перечисленных в разделе "Файлы".)
Например:
[files]
top.sv
../common/defines.vh
/data/prj42/modules/foobar.sv
sby скопирует эти файлы как top.v, defines.vh, и foobar.sv в <outdir>/src/.
Если имя файла в <outdir>/src/ должно отличаться от базового имени указанного файла, тогда новое имя файла может быть указано перед именем исходного файла. Например:
[files]
top.sv
defines.vh ../common/defines_footest.vh
foo/bar.sv /data/prj42/modules/foobar.sv
Разделы файла
Разделы файла могут быть использованы для создания дополнительных файлов в <outdir>/src/ из буквального содержания [file <filename>]. Для примера:
[file params.vh]
`define RESET_LEN 42
`define FAULT_CYCLE 57
Команда: sby --dumpcfg <sby_file> может использоваться для печати в конфигурации без указания на какую-либо конкретную задачу, и sby --dumpcfg <sby_file> <task_name> может использоваться для печати конфигурации со специализацией для конкретной задачи.
Формальные испытания
Для проведения формальных испытаний создадим файл .sby в соответствии с выше изложенными правилами.
[tasks]
yices
[options]
mode prove
depth 20
[engines]
yices: smtbmc yices
[script]
read_verilog -formal sum_n.v
prep -top sum_n -nordff
[files]
sum_n.v
Где
-
yices это имя задачи, которое может быть произвольным:
-
smtbmc движок с решателем yices:
-
указываем скрипту read_verilog прочитать файл sum_n.v раздел formal;
-
определяем имя топ модуля -top sum_n;
-
и в секции [files] указываем исходный файл.
Здесь мы определяем одну задачу yices и движок для её исполнения smtbmc с решателем yices. Само имя задачи может быть произвольным. Также мы задаём некоторые настройки: mode prove - режим доказательства и depth 20 - количество повторений.
Добавим в файл модуля секцию FORMAL. Это мы сделаем в соответствии с описанием:
module somemodule(port1, port2, ...);
// User logic here
//
`ifdef FORMAL
// Formal properties here
`endif
endmodule
Данное описание приведено в документации на SymbiYosys. Здесь секция FORMAL используется для отделения раздела, имеющего формальные свойства, от остальной логики в модуле. Что же мы будем сюда добавлять? Познакомимся с основными немедленными утверждениями SystemVerilog.
Немедленные утверждения SystemVerilog
-
assume(<expr>);
Предположение ограничивает возможности, которые исследует формальный инструмент, уменьшая пространство поиска. В любой трассировке, сгенерированной solver, все предположения всегда будут верными.
-
assert(<expr>);
Утверждение - это то, что решатель попытается сделать ложным. В любое время SymbiYosys запускается с mode bmc, доказательство завершится неудачей, если некоторый набор входных данных может вызвать <expr> в пределах утверждения, равного нулю (false). При запуске SymbiYosys с mode prove, доказательство также может привести к UNKNOWN результату, если утверждение может быть выполнено с ошибкой во время шага индукции.
-
cover(<expr>);
Оператор cover применяется только в том случае, если SymbiYosys запускается с параметром mode cover. В этом случае формальный решатель запустится в начале времени (т.е. Когда все начальные утверждения верны), и он будет пытаться найти некоторые часы, когда <expr> можно сделать так, чтобы это было правдой. Такой прогон покрытия “ПРОЙДЕТ”, как только все внутренние cover() заявления будут выполнены . Произойдет “СБОЙ”, если существует утверждение, которое не может быть достигнуто в первые N состояний, где N устанавливается с помощью depth опция. Повторный проход также завершится неудачей, если потребуется выполнить утверждение, при котором состояние будет прерванным, чтобы достичь полного покрытия.
Вот эти утверждения мы и будем добавлять в секцию FORMAL
module sum_n (port1, port2, ...);
...
`ifdef FORMAL
// Formal properties here
localparam [2:0] FORMAL_TEST = 3'b000;
case (FORMAL_TEST)
3'b000: begin
always @(*) begin
assume(s_out ≥ 1);
end
end
3'b001: begin
// No extra logic
// Never passes
end
endcase
`endif
endmodule
В дальнейшем, здесь можно будет добавить и другие свойства и условия проверки. Сейчас мы делаем совершенно очевидное утверждение: сумма ряда натуральных чисел должна быть как минимум больше или равна 1.
3'b000: begin
always @(*) begin
assume(s_out ≥ 1);
end
end
Проверим модуль.
$sby -f sum_n.sby
...
SBY 17:39:04 [sum_n_yices] summary: engine_0 (smtbmc yices) returned pass for basecase
SBY 17:39:04 [sum_n_yices] summary: engine_0 (smtbmc yices) returned pass for induction
SBY 17:39:04 [sum_n_yices] summary: engine_0 did not produce any traces
SBY 17:39:04 [sum_n_yices] summary: successful proof by k-induction.
SBY 17:39:04 [sum_n_yices] DONE (PASS, rc=0)
Ничего неожиданного мы здесь не получили, но и sby ничего неожиданного не ищет, поскольку мы задали лишь предположение assume без ограничений assert, то есть решатель и не пытается сделать что-либо ложным. Какое же ограничение задать? Посмотрим на исходную формулу. Первое необходимое ограничение задано прямо в этой формуле. Добавим его в FORMAL.
b000: begin
always @(*) begin
assume(s_out ≥ 1);
assert(n_in ≥ m_in);
end
end
И проверим модуль. И тут же получаем ошибку.
SBY 18:21:01 [sum_n_yices] summary: engine_0 (smtbmc yices) returned FAIL for basecase
SBY 18:21:01 [sum_n_yices] summary: counterexample trace [basecase]: sum_n_yices/engine_0/trace.vcd
SBY 18:21:01 [sum_n_yices] summary: failed assertion sum_n.$assert$sum_n.v:32$16 at sum_n.v:32.22-36.23 in step 0
SBY 18:21:01 [sum_n_yices] DONE (FAIL, rc=2)
SBY 18:21:01 The following tasks failed: ['yices']
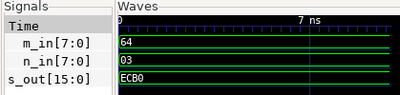
Что же не так? Мы, ведь, задали правильное условие, но получили ошибку. Всё так! Программа sby действует как хороший хакер. Она пытается обойти правильные пути, ищет то, что можно сломать, то, что можно сделать не так. Открываем файл в gtkwave и смотрим эпюры.
Здесь видно, что n<m, тогда как мы задали n ≥ m Мы задали правильное условие, но в модуле не предусмотренно ни каких ограничений на вводимые данные. Поэтому первое, что делает решатель - он допускает, что раз в модуле нет ограничений, то можно задать не правильные данные. Решатель ничего не знает об окружении модуля. Но решатель видит, что нет ограничений и подставляет не правильные данные.
Что же, отправим модуль на доработку. Получив модуль обратно, посмотрим на внесённые изменения.
assign s_out = (n_in ≥ m_in)?(m_in + n_in) * (n_in - m_in + 1) / 2:0;
Видно, что инженер быстро внёс минимальные изменения. Это позволяет в самом модуле отслеживать условие n ≥ m и не допускать некорректных решений, возвращая 0 в случае не соблюдения условия. В проверочном стенде теперь можно убрать ограничение на подаваемые в модуль данные.
Запустим формальную проверку.
SBY 17:36:22 [sum_n_yices] summary: engine_0 (smtbmc yices) returned pass for basecase
SBY 17:36:22 [sum_n_yices] summary: engine_0 (smtbmc yices) returned pass for induction
SBY 17:36:22 [sum_n_yices] summary: engine_0 did not produce any traces
SBY 17:36:22 [sum_n_yices] summary: successful proof by k-induction.
SBY 17:36:22 [sum_n_yices] DONE (PASS, rc=0)
Мы легко справились с ошибкой в первом ограничении. И казалось бы всё хорошо. Но давайте ещё раз внимательно посмотрим на ограничения, которые мы хотим проверить. Здесь задано соотношение между n и m, и задана надежда, что результат должен быть больше 0. Но просмотрим на исходную формулу. Ведь мы работаем с натуральным рядом чисел без 0. Но, в этом смысле у нас нет ограничений. Давайте их введём.
assert(m_in > 0); assert(n_in > 0);
Здесь мы показали, что ∀n, m ∈ ℕ. В очередной раз запускаем проверку и получаем
DONE (FAIL, rc=2)
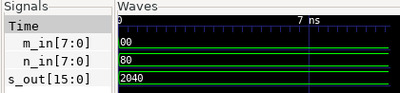
В чём же дело? Ведь мы совершенно правильно указали, что числа должны принадлежать натуральному ряду без 0. Смотрим эпюры.
Здесь видно, что решатель нашёл, и довольно быстро нашёл, возможность подать 0 на шину m_in. Почему он это сделал? Ну мы ему об этом так прямо и сказали: "проверь ограничение m_in>0 (assert(m_in>0);)." Как можно проверить ограничение? Подать ему на вход что-нибудь не соответствующее ожиданиям. Не правда ли? Составляем протокол и отдаём модуль на доработку. Через некоторое время получаем доработанный модуль.
assign s_out = (n_in ≥ m_in) & (n_in > 0) & (m_in > 0)?(m_in + n_in) * (n_in - m_in + 1) / 2:0;
И протокол работы устройства.
$ vvp a.out
VCD info: dumpfile out.vcd opened for output.
A= 99 B= 9 S= 0, 0x0
A=141 B= 13 S= 0, 0x0
A= 18 B=101 S= 4998, 0x1386
A= 13 B= 1 S= 0, 0x0
A= 61 B=118 S= 5191, 0x1447
A=140 B=237 S=18473, 0x4829
A=198 B=249 S=11622, 0x2d66
A=170 B=197 S= 5138, 0x1412
A=119 B=229 S=19314, 0x4b72
sum_n_tb.v:32: $finish called at 190000 (1ps)
A=119 B=229 S=19314, 0x4b72
Видно, что наш модуль по прежнему хорошо справляется со своей задачей.
Проведём снова формальную проверку.
SBY 18:09:11 [sum_n_yices] summary: engine_0 (smtbmc yices) returned pass for basecase
SBY 18:09:11 [sum_n_yices] summary: engine_0 (smtbmc yices) returned pass for induction
SBY 18:09:11 [sum_n_yices] summary: engine_0 did not produce any traces
SBY 18:09:11 [sum_n_yices] summary: successful proof by k-induction.
SBY 18:09:11 [sum_n_yices] DONE (PASS, rc=0)
Модуль успешно проходит тест, справляясь с потоком данных в полном соответствии с заданной формулой. Таким образом мы доказали, что выражение
assign s_out = (n_in ≥ m_in) & (n_in > 0) & (m_in > 0)? (m_in + n_in) * (n_in - m_in + 1) / 2:0;
эквивалентно заданной формуле, что можно записать как
∀n, m ∈ ℕ (n≥m): P(s) ≡ P(n)
Следовательно, поскольку предикат P(s) представляет собой высказывание о модуле sum_n и эквивалентен предикату P(n) представляющему высказывание о формуле и оба они являются истинными высказываниями, то и модуль как высказывание о формуле тоже является истинным высказыванием в том виде к которому он быд приведён.
Посмотрим на проделанную работу.
- Получено первое представление о том, что такое SymbiYosys (sby).
- Проделан цикл работ по разработке, отладке и формальной проверке цифрового модуля.
- Была показана идея, как работает формальная проверка.
- Также, было показано, что модуль sum_n работает правильно при любых допустимых n и m.
Код на гите sum_n
Автор приветствует конструктивные замечания и предложения по вопросам, затронутым в статье. Может, кто-нибудь из читателей найдёт в этом модуле ещё, по крайней мере одно недопустимое состояние?
С уважением, Сергей.
@SergeBN