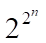Найдено 9-ое число Дедекинда и, как вы наверное догадываетесь, не без помощи FPGA
42 цифры создающие историю. Ученые из Университета Paderborn и KU Leuven раскрыли тайну математики десятилетней давности, относящуюся к так называемым числам Дедекинда.
Эксперты по всему миру занимаются поиском 9-го числа Дедекинда с 1991 года. Ученые из университета Paderborn получили точную последовательность чисел с помощью расположенного там суперкомпьютера Noctua. Результаты будут представлены в сентябре на Международном семинаре по булевым функциям и их приложениям (BFA) в Норвегии.
То, что начиналось как магистерский дипломный проект Леннарта Ван Хиртума, в то время студента-информатика в университете Левена, а ныне научного сотрудника в Университете Падерборна, стало огромным успехом. Предыдущие числа были найдены самим Ричардом Дедекиндом, когда он впервые сформулировал задачу в 1897 году, а позже такими великими представителями ранней информатики, как Рэндольф Черч и Морган Уорд. "В течение 32 лет вычисление D(9) (девятое число Дедекинда) было открытой задачей, и было сомнительно, удастся ли вообще когда-либо вычислить это число", - говорит Ван Хиртум.
Предыдущее число в последовательности Дедекинда, 8-е число Дедекинда, было найдено в 1991 году с помощью Cray 2, самого мощного суперкомпьютера того времени. "Поэтому это казалось вполне возможным, что к настоящему времени должно быть возможно вычислить 9-е число на большом суперкомпьютере", - говорит Ван Хиртум, описывая мотивацию амбициозного проекта, который он первоначально реализовал совместно с руководителями своей магистерской диссертации в университете Левена.
Песчинки, шахматы и суперкомпьютеры
Основным предметом изучения чисел Дедекинда являются так называемые монотонные булевы функции. Ван Хиртум объясняет: "В принципе, вы можете представить монотонную булеву функцию в двух, трех и бесконечных измерениях как игру с n-мерным кубом. Вы балансируете куб на одном углу, а затем окрашиваете каждый из оставшихся углов либо в белый, либо в красный цвет. Есть только одно правило: вы никогда не должны располагать белый угол над красным. Это создает своего рода вертикальное красно-белое пересечение.
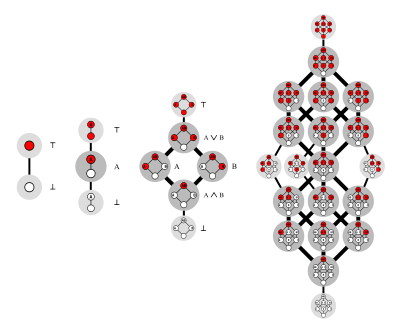
Картинка из википедии
"Цель игры состоит в том, чтобы подсчитать, сколько существует различных разрезов. Их число - это то, что определяется как число Дедекинда. Даже если кажется, что это не так, цифры в процессе быстро становятся гигантскими: 8-е число Дедекинда уже состоит из 23 цифр."
Сравнительно большие — но несравнимо более простые в вычислении — числа известны из легенды, связанной с изобретением игры в шахматы. "Согласно этой легенде, изобретатель шахматной игры попросил у короля в награду всего несколько зернышек риса на каждом квадрате шахматной доски: одно зернышко на первом квадрате, два зернышка на втором, четыре на третьем и вдвое больше на каждом из следующих квадраты. Король быстро понял, что эту просьбу выполнить невозможно, потому что такого количества риса не существует во всем мире.
"Количество рисовых зерен на полной доске будет состоять из 20 цифр — невообразимое количество, но все же меньше, чем D(8). Когда вы осознаете эти величины, становится очевидно, что для нахождения D (9) потребовался бы как эффективный вычислительный метод, так и очень быстрый компьютер", - сказал Ван Хиртум.
Годы превращаются в месяцы
Для вычисления D(9) ученые использовали методику, разработанную научным руководителем магистерской диссертации Патриком Де Каусмекером, известную как формула P-коэффициента. Это обеспечивает способ вычисления чисел Дедекинда не путем подсчета, а с помощью очень большой суммы. Это позволяет декодировать D(8) всего за восемь минут на обычном ноутбуке. Но "То, что занимает восемь минут для D(8), становится сотнями тысяч лет для D(9). Даже если бы вы использовали большой суперкомпьютер исключительно для этой задачи, все равно потребовалось бы много лет, чтобы завершить вычисления", - отмечает Ван Хиртум.
Основная проблема заключается в том, что количество слагаемых в этой формуле растет невероятно быстро. "В нашем случае, используя симметрии в формуле, мы смогли сократить количество слагаемых "всего" до 5,5x1018 — огромное количество. Для сравнения, количество песчинок на Земле составляет около 7,5х1018, но для современного суперкомпьютера операции размером 5,5х1018 вполне выполнимы", - сказал специалист по информатике.
Проблема: вычисление этих слагаемых на обычных процессорах происходит медленно, а использование графических процессоров ( в настоящее время это самая быстрая технология аппаратного ускорения для многих приложений искусственного интеллекта) неэффективно для этого алгоритма.
Решение: Аппаратные ресурсы для конкретного приложения, использование узкоспециализированных и параллельных арифметических блоков в ПЛИС (программируемых логических интегральных схем). Ван Хиртум разработал первоначальный прототип аппаратного ускорителя и начал искать суперкомпьютер, оснащенный необходимыми ПЛИС-картами. В процессе работы он узнал о компьютере Noctua 2 в "Падерборнском центре параллельных вычислений (PC2)" при Университете Падерборна, который располагает одной из самых мощных в мире систем FPGA (в оригинале FPGA systems :) ).
Профессор Кристиан Плессл, руководитель PC2, объясняет: "Когда Леннарт Ван Хиртум и Патрик Де Каусмакер связались с нами, нам сразу стало ясно, что мы хотим поддержать этот проект. Решение сложных комбинаторных задач с помощью ПЛИС является многообещающей областью применения, и Noctua 2 - один из немногих суперкомпьютеров во всем мире, с которым вообще возможен такой эксперимент. Экстремальные требования к надежности и стабильности также представляют собой проблему и испытание для нашей инфраструктуры. Команда экспертов-консультантов по ПЛИС тесно сотрудничала с Леннартом, чтобы адаптировать и оптимизировать приложение под наше окружение".
После нескольких лет разработки программа работала на суперкомпьютере около пяти месяцев. И вот пришло время: 8 марта ученые обнаружили 9-е число Дедекинда: 286386577668298411128469151667598498812366.
Сегодня, спустя три года после начала проекта Dedekind, Ван Хиртум работает научным сотрудником Высшей школы NHR в Падерборнском центре параллельных вычислений над разработкой следующего поколения аппаратных средств в рамках своей докторской диссертации. Высшая школа NHR (National High Performance Computing) является совместной высшей школой NHR (National High Performance Computing). Центры NHR. Он расскажет о своем необычайном успехе вместе с Патриком Де Каусмекером 27 июня в 14:00 в лекционном зале O2 Университета Падерборна.