NaN boxing
Зачем же боксируют между собой значения NaN и что им друг от друга нужно? Давайте вспомним значения битовых полей в представлении чисел в формате IEEE-754 [рассмотрим 32/64-битные случаи].
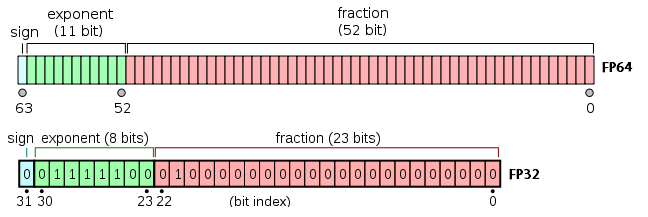
fp64/32 - это double и float соответственно
Битовая строка для формата IEEE-754 состоит из трех полей: поле знака, поле экспоненты, поле мантиссы [если будет интерес к тому почему для стандарта выбрали именно такие поля и какой в них математический смысл - пишите, обсудим это в последующих заметках]. Например число записанное в виде 0x40080000, ничто иное как число 2,125. [ссылка на конвертер]
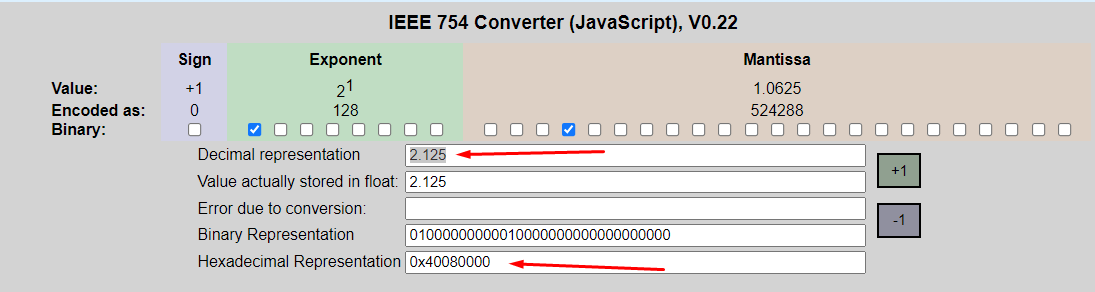
Двоичное представление числа представлено на картинке ниже.

В далеком 1985-м году, когда был утвержден первый стандарт представления чисел с плавающей точкой для ЭВМ, в нем было введены операции с NaN. NaN, в свою очередь, разделяются на 2 подмножества: qNaN [тихие NaN] и sNaN [сигнальные NaN]. В чем же различие между ними? Давайте обратимся к стандарту 1985-го года.
Когда упоминаются годы выпуска стандарта: 1985, 2008 - не стоит это воспринимать, как два абсолютно разных и не зависимых стандарта. IEEE-754 1985/2008/2019 все обратно совместимы друг с другом. В контексте данной статьи год выпуска стандарта не играет какой-либо существенной роли и упоминается он только для того, чтобы показать, что разработка стандарта IEEE-754 не стоит на месте.
Из стандарта следует, что sNaN сигнализирует [он же все таки signaling] о произошедшей недопустимой операции, например, деление на нуль, извлечение квадратного корня из отрицательного числа.
Кстати, а вы никогда не задумывались, а почему корень квадратный? Вы же видели корни деревьев, мне кажется они совсем не квадратные. Крутая этимологическая заметка - тут
Для всех этих недопустимых операций возвращается sNaN, генерирующий прерывания. Сигналы формата qNaN в далеких 80-х служили отладочной информацией для разработчиков, помогали находить проблемные места, ошибки в вычислениях/алгоритмах. На сегодняшний день с современными средствами отладки и моделирования актуальность армии NaN'ов [по крайней мере, в текущем виде] остается под вопросом.
На практике многие разработчики микропроцессоров по своему воспринимают и обрабатывают qNaN/sNaN и отходят от определений стандарта. Как видно из функции ниже, в зависимости от порядка скобок операция minNum в одном случае возвращает 1, а в другом qNaN [в 2019-м стандарте IEEE-754 данная операция была заменена аналогичной, математически корректной функцией].
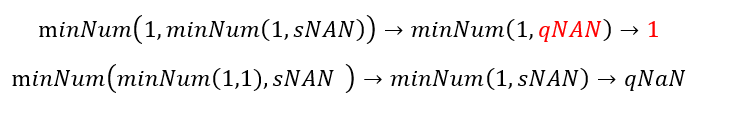
Ниже приведена сравнительная таблица, где рассматривается скандальная операция fmin [IEEE-754-2008] и как она имплементирована в различных компиляторах, процессорах.
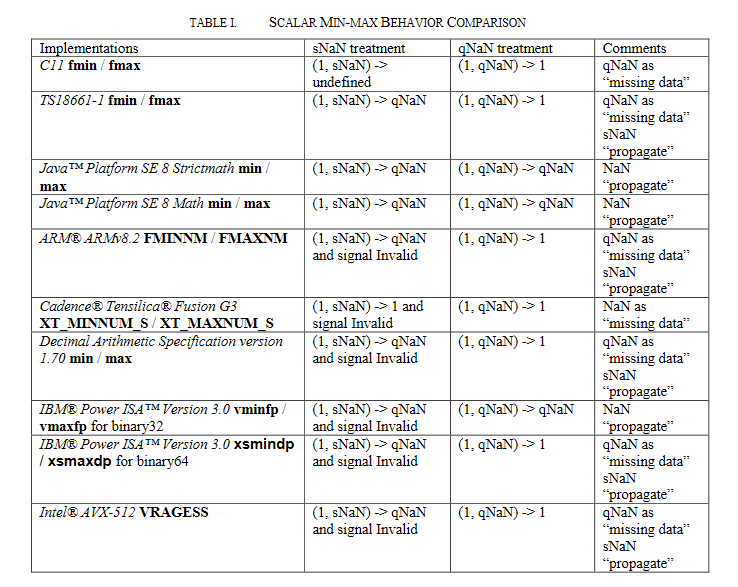
Ранее мы рассмотрели битовые поля стандарта IEEE-754. Теперь рассмотрим, как NaN записываются в битовой строке.

Как мы видим из таблицы выше, представление NaN - это экспонента, "забитая" единицами, и ненулевое представление дробной части (она же мантисса, она же fraction).
Мы разобрались с идеей представление NaN в формате IEEE-754. Может возникнуть вопрос, а как же различить qNaN и sNaN? Ответ - старшим битом мантиссы. Для qNaN, он равен 1, для sNaN - 0.

Теперь, когда мы закрыли необходимый минимальный теоретический бэкграунд по вопросам представления и обработки NaN, вернемся к началу нашей статьи, а именно - что же такое NaN boxing и зачем он нужен?
В данной главе вводится понятие регистрового файла для float-point значений. Регистровый файл неотъемлемая часть load-store архитектуры, которой и являются RISC-процессоры. Это маленькая, но самая быстрая память из тех, что доступна процессору. Там хранятся значения целочисленных операций, значения адреса верхушки стэка, константный нуль [справедливо, для RISC-V архитектуры], некоторые регистры хранят в себе аргументы функций, коды системных вызовов.
Перегружать уже существующий регистровый файл результатами вычислений с плавающей точкой не лучшая затея. Поэтому для расширений F/D вводится регистровый файл для операций с плавающей точкой.
Обратимся к стандарту RISC-V - нас интересует документ с таким названием "Volume 1, Unprivileged Spec v". В 11 главе начинается обзор расширения F [float].

В нем представлено 32 регистра [от f0 до f31] шириной FLEN, и fcsr - статусный регистр, хранящий информацию о режиме округления, исключениях и.т.д. Нас интересует параметр FLEN. Из названия легко догадаться, что данный параметр отвечает за ширину [разрядность] битовой строки в регистровом файле. Обратимся к стандарту:
FLEN can be 32, 64, or 128 depending on which of the F, D, and Q extensions are supported. There can be up to four different floating-point precisions supported, including H, F, D, and Q.
Тут H,F,D,Q - описание представлений fp чисел: half, float, double, quadro.
Давайте рассмотрим такой пример. Нам поставили задачу доработать процессор, поддерживающий архитектуру RV32IF, до архитектуры RV32IFD. То есть, фактически, добавить поддержку расширения double, чтобы была возможность обрабатывать 64-битные числа с плавающей точкой. Задача на уровне FPU решается относительно просто - расширяем существующие вычислители для поддержки double, увеличиваем ширину битовых полей, добавляем мультиплексоры для маскирования результата, разрабатываем логику чтобы отличать float от double.
А что же делать с параметром FLEN для регистрового файла fp чисел? Нам нужно создать еще один регистровый файл? Как нам поступить? Создание лишнего блока накристальной памяти дорого, энергозатратно, отнимает драгоценную площадь. Да и смысла нет в том, чтобы плодить идентичные блоки, а не переиспользовать текущие, особенно если это никак не скажется на производительности нашего чипа.
Что будет, если мы будем хранить все значения и float и double в нашем регистровом файле с FLEN = 64? Отлично, но как различить float и double? Например, мы записали уже знакомое нам число 2,125 [0x40080000 в формате float] в 64-битный регистровый файл. Далее, следующая операция по какой-либо причине обращается к данной ячейке памяти и считывает 64-битное число формата double и получает в результате субнормальное число 5,307579804e-315.
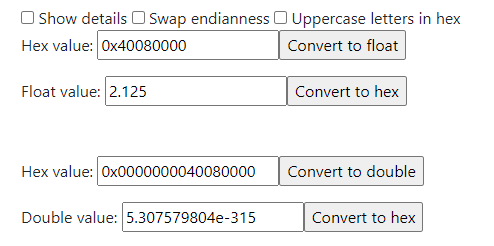
Почему так произошло? Все наши 32 бита, где были закодированы: знак, экспонента, мантисса присвоились в поле 52 битной мантиссы double числа. В данном случае поле, отвечающее за экспоненту, осталось не перезаписанным, а именно нулевым. По итогу мы получили субнормальное число отличающееся от нашего на пару сотен порядков.

Как же нам избежать данной проблемы?
Снова обратимся к стандарту RISC-V:
When multiple floating-point precisions are supported, then valid values of narrower n-bit types, n < FLEN, are represented in the lower n bits of an FLEN-bit NaN value, in a process termed NaN-boxing. The upper bits of a valid NaN-boxed value must be all 1s. Valid NaN-boxed n-bit values therefore appear as negative quiet NaNs (qNaNs) when viewed as any wider m-bit value, n < m ≤ FLEN. Any operation that writes a narrower result to an f register must write all 1s to the uppermost FLEN−n bits to yield a legal NaN-boxed value
Ответ крайне прост, когда число меньшей разрядности [например float разрядность 32] записывается в регистровый файл, то следует расширить наше число до нужной разрядности, добавив в старшую часть 1. Например, если мы записывали число 32-битное число 32'h40080000 [представление числа на языке описания аппаратуры Verilog - эквивалентно 0x40080000], то нам следует расширить его до 64-битного следующим образом - {32'hFFFF_FFFF, 32'h40080000} - данная запись эквивалентна 0xFFFFFFFF4008000.
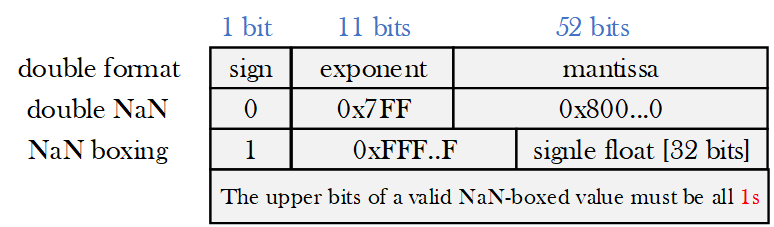
И тогда при считывании double числа из данного регистра мы получим уже NaN - предупреждение о том, что мы что-то делаем не так.

А при чтении float-числа из данной ячейки, мы считаем только младшие 32 бита 64-битного числа, что нам даст верный ответ.
Если вам показалась данная заметка интересной и вам хотелось бы поподробнее изучить специфику работы арифметики с плавающей точкой, то рекомендую ознакомиться со следующими материалами:
- Учебный курс на русском языке по IEEE-754
- Настольная книга разработчика fp-вычислителей - Handbook of Floating-Point Arithmetic
p.s. За вычитку статьи, советы в оформлении выражаю благодарность: Михаилу Попову, Анне Михайловой, Денису Габидуллину, Ивану Шевчуку.
Телеграм канал автора: Записки CPU designer'a: https://t.me/cpu_design
p.p.s. если у вас есть вопросы / предложения со мной всегда можно связаться тут:
- в twitter: https://twitter.com/NickTernovoy
- в linkedin: https://www.linkedin.com/in/nickolay-ternovoy-8130011ab/
ppps: Кстати, автор делал доклад на нашей первой FPGA конференции. Рекомендуется к ознакомлению